Regresyon Yöntemleri
FEF3001 Yapay Zekaya Giriş - Ders 6
2024-07-25
İçerik
- Regresyonun tanımı
- Regresyon türleri (doğrusal, polinom ve topluluk yöntemleri)
- Doğrusal Regresyon: Basit Doğrusal Regresyon, En Küçük Kareler yöntemi, Model performansının değerlendirilmesi (R-kare, RMSE)
- Polinom Regresyon: Ne zaman polinom regresyon kullanılır, aşırı uyum
- Rastgele Orman ile Regresyon: Regresyon için Rastgele Orman algoritması, Avantajları (doğrusal olmayan ilişkileri ele alma, özellik önemi)
- Diğer regresyon türleri: Lojistik regresyon (ikili sonuçlar için), Ridge ve Lasso regresyonu (düzenlileştirme teknikleri)
- Excel’de örnekler
- R ve Python’da kod örnekleri
Regresyon
Regresyon, bir bağımlı değişken (genellikle hedef veya sonuç değişkeni olarak adlandırılır) ile bir veya daha fazla bağımsız değişken (ayrıca tahmin edici veya özellik olarak da bilinir) arasındaki ilişkiyi modellemek ve analiz etmek için veri analizinde ve makine öğrenmesinde kullanılan istatistiksel bir yöntemdir. Regresyonun temel amacı, bağımsız değişkenlerdeki değişikliklerin bağımlı değişkendeki değişikliklerle nasıl ilişkili olduğunu tahmin etmek ve çıkarım yapmaktır.
Regresyon hakkında önemli noktalar:
- Değişkenler arasındaki ilişkileri tanımlamaya ve ölçmeye yardımcı olur.
- Hem tahmin hem de değişkenlerin etkisini anlamak için kullanılabilir.
- Doğrusal, polinom ve Rastgele Orman veya regresyon için Sinir Ağları gibi daha karmaşık yöntemler dahil olmak üzere çeşitli regresyon türleri vardır.
- Regresyon modelleri hem sürekli hem de kategorik değişkenleri ele alabilir.
- Bilim, ekonomi ve sosyal bilimler dahil olmak üzere birçok alanda yaygın olarak kullanılır.
Doğrusal (Lineer) Regresyon
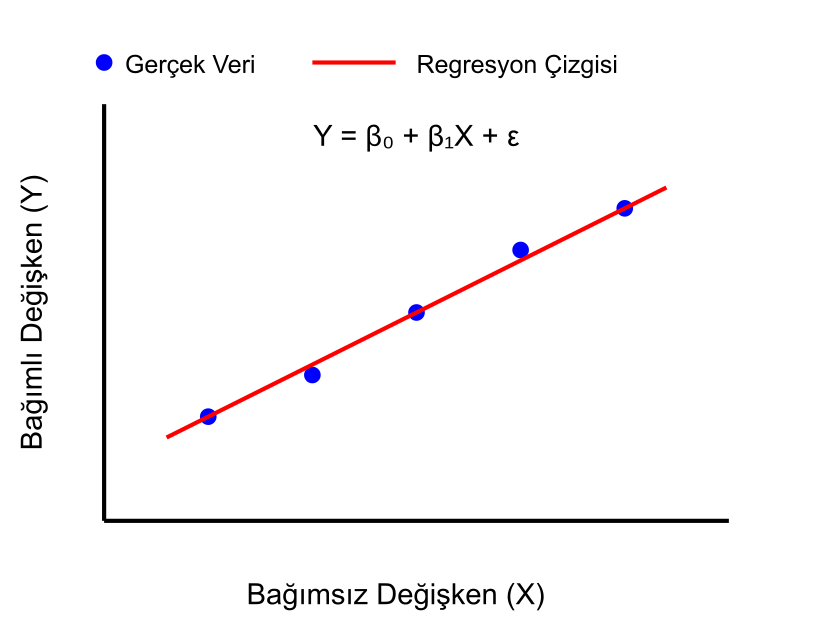
Doğrusal Regresyon
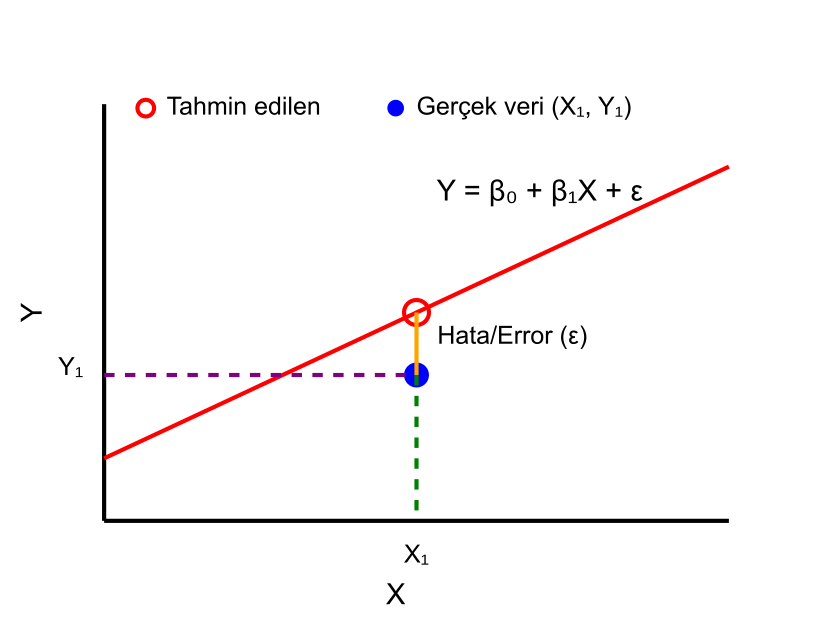
Doğrusal Regresyon
En iyi doğruyu bulmayı deneyin: https://www.geogebra.org/m/xC6zq7Zv
En Küçük Kareler (OLS) Yöntemi
En Küçük Kareler (Ordinary Least Squares - OLS), doğrusal bir regresyon modelinin parametrelerini tahmin etmek için kullanılan istatistiksel bir yöntemdir. Doğrusal regresyonda bir veri kümesine doğru yerleştirmek için en yaygın kullanılan tekniktir.
OLS, gözlemlenen bağımlı değişken değerleri ile bağımsız değişken(ler)in doğrusal fonksiyonu tarafından tahmin edilen değerler arasındaki farkların karelerinin toplamını en aza indiren bir yöntemdir. Başka bir deyişle, kare artıkların toplamını en aza indirerek verilere en iyi uyan çizgiyi (veya çoklu boyutlarda hiperplane) bulur.
Teknik detaylar için lütfen Wikipedia’daki OLS Yöntemi sayfasını ziyaret edin.
Çok Değişkenli Doğrusal Regresyon
Çok Değişkenli Doğrusal Regresyon, aynı zamanda Çoklu Doğrusal Regresyon olarak da bilinen, birden fazla bağımsız değişken ile tek bir bağımlı değişken arasındaki ilişkiyi modellemek için kullanılan istatistiksel bir yöntemdir. Basit doğrusal regresyon kavramını birden fazla tahmin değişkeni içerecek şekilde genişletir.
Modelin genel formu şöyledir:
\[ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_nx_n + \varepsilon \]
Burada:
y bağımlı değişken, x₁, x₂, …, xₙ bağımsız değişkenler, β₀ y-kesişimi (tüm x’ler sıfır olduğunda y’nin değeri), β₁, β₂, …, βₙ her bağımsız değişkenle ilişkili katsayılar, n bağımsız değişken sayısı, ε hata terimi
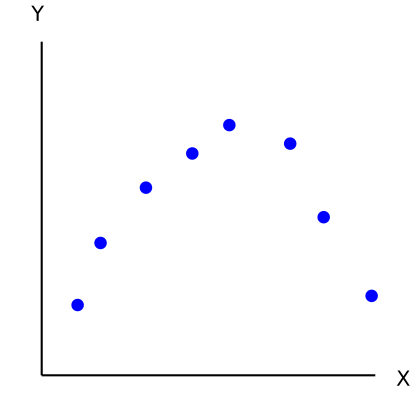
Polinom Regresyon
Polinom Regresyon, bağımsız değişken x ile bağımlı değişken y arasındaki ilişkinin n’inci dereceden bir polinom olarak modellendiği bir regresyon analizi formudur. Değişkenler arasındaki ilişki doğrusal olmadığında ancak bir polinom fonksiyonuyla yaklaşık olarak ifade edilebileceği durumlarda kullanılır.
\[ y = \beta_0 + \beta_1x + \beta_2x^2 + \beta_3x^3 + \ldots + \beta_nx^n + \varepsilon \]
Burada:
y bağımlı değişken, x bağımsız değişken, β₀, β₁, β₂, …, βₙ tahmin edilecek katsayılar, n polinomun derecesi ve ε hata terimi
Polinom Regresyon
Excel’de Doğrusal Regresyon
MTCARS veri seti Excel dosyasını kullanın ve;
- wt (ağırlık) ve mpg (galon başına mil) sütunları arasında Eğilim Çizgisi çizin.
- disp (silindir hacmi) ve wt (ağırlık) sütunları arasında Eğilim Çizgisi çizin.
Excel’de nasıl Eğilim Çizgisi çizileceğini görmek için lütfen MyExcelOnline sayfasını ziyaret edin.

R ile Doğrusal Regresyon
Basit doğrusal ve polinom regresyon için lütfen R ile Doğrusal Regresyon sayfasına bakın.
Rastgele Orman (Random Forest) ile Regresyon
Lütfen R ile rastgele orman regresyonu belgesine bakın.