Kümeleme Yöntemleri
FEF3001 Yapay Zekaya Giriş - Ders 7
2024-07-26
İçerik
- Kümelemeye Giriş
- Tanım ve amaç, Denetimsiz öğrenme kavramı, Bilimsel alanlardaki gerçek dünya uygulamaları
- Kümeleme Algoritmaları Türleri
- Bölümleme yöntemleri (örn. K-means)
- Hiyerarşik yöntemler
- Yoğunluk tabanlı yöntemler (örn. DBSCAN)
- K-means Kümeleme
- Algoritma açıklaması
- Küme sayısını seçme (dirsek yöntemi)
- Avantajlar ve sınırlamalar
- Hiyerarşik Kümeleme
- Birleştirici ve bölücü yaklaşımlar
- Dendrogram yorumlama
- Bağlantı yöntemleri (tek, tam, ortalama)
- Yoğunluk Tabanlı Mekansal Gürültülü Uygulama Kümelemesi (DBSCAN)
- Temel kavramlar: çekirdek noktalar, sınır noktalar, gürültü
- Algoritma açıklaması
- Avantajlar
- Kümeleme için Değerlendirme Metrikleri
- Silüet skoru
Tanım
Kümeleme, makine öğrenmesi ve veri analizinde bir dizi nesneyi veya veri noktasını, aynı gruptaki (küme olarak adlandırılır) nesnelerin diğer gruplardakilere göre birbirine daha benzer olacağı şekilde gruplandırmayı içeren bir tekniktir. Bu, birçok veri analizi ve örüntü tanıma probleminde temel bir görevdir.
Amaç
Kümelemenin amacı çok yönlüdür:
Örüntü Keşfi: Kümeleme, veriler içindeki hemen belli olmayan doğal örüntüleri veya yapıları tanımlamaya yardımcı olur.
Veri Özetleme: Büyük veri setlerini, birçok veri noktasını daha az küme merkeziyle temsil ederek sıkıştırmak için kullanılabilir.
Anomali Tespiti: Benzer veri noktalarının gruplarını tanımlayarak, herhangi bir kümeye uymayan aykırı değerleri veya anormallikleri tespit etmeye yardımcı olabilir.
Segmentasyon: Pazarlama gibi alanlarda, müşterileri benzer davranışlara veya özelliklere sahip gruplara ayırmak için kullanılır.
Diğer Algoritmalar için Ön İşleme: Kümeleme, verinin karmaşıklığını azaltmak için diğer algoritmalar için bir ön işleme adımı olarak kullanılabilir.
Doğal Sınıflandırma: Bilimsel alanlarda, kümeleme verilerdeki doğal gruplandırmaları ortaya çıkarabilir, örneğin biyolojide benzer türleri gruplandırmak veya astronomide yıldız türlerini kategorilere ayırmak için.
Kümeleme Yöntemleri
Bölümleme yöntemleri: Veriyi örtüşmeyen alt kümelere böler, her veri noktası tam olarak bir kümeye ait olur, genellikle belirli bir kriteri optimize eder.
Hiyerarşik Yöntemler: Küçük kümeleri daha büyük olanlarla birleştirerek veya büyük kümeleri daha küçük olanlara bölerek kümelerin ağaç benzeri bir yapısını oluşturur.
Yoğunluk tabanlı Yöntemler: Yüksek veri noktası yoğunluğu olan alanlarda kümeler oluşturur, düşük yoğunluklu bölgelerle ayrılır, keyfi şekilli kümelerin keşfine olanak tanır.
Uygulamalar
- Biyoloji
- Gen İfadesi Analizi: Farklı koşullar veya zaman noktaları arasında benzer ifade kalıplarına sahip genleri gruplandırma.
- Tür Sınıflandırması: Organizmaları genetik veya morfolojik özelliklere göre kümeleme.
- Protein Yapısı Analizi: Proteinlerde yapısal motifleri tanımlama.
- Kimya
- Moleküler Dinamikler: Simülasyonlar sırasında moleküllerin konformasyonlarını analiz etme.
- Spektroskopi: Bileşik tanımlama için benzer spektrumları kümeleme.
- İlaç Keşfi: Benzer özelliklere veya etkilere sahip kimyasal bileşikleri gruplandırma.
- Fizik
- Parçacık Fiziği: Yüksek enerjili fizik deneylerinde parçacık çarpışma olaylarını sınıflandırma.
- Astrofizik: Yıldızları veya galaksileri özelliklerine göre (örn. parlaklık, sıcaklık) kümeleme.
- Malzeme Bilimi: Malzemelerdeki kristal yapıları ve kusurları analiz etme.
Bölümleme
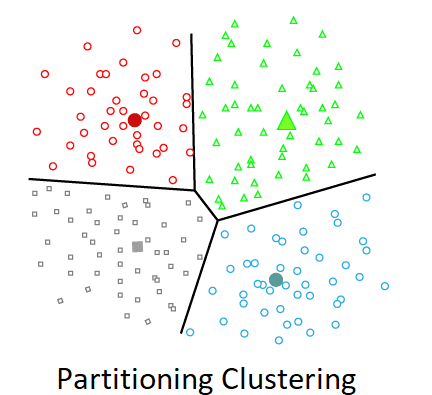
K-means kümeleme
K-means kümeleme, benzer veri noktalarını kümelere gruplandırmak için kullanılan denetimsiz bir makine öğrenimi algoritmasıdır. Veri noktalarını, küme merkezlerine (merkezoidlere) olan benzerliklerine göre önceden tanımlanmış k kümeye iteratif olarak atayarak çalışır. Algoritma, özellik uzayında k merkezoidi rastgele başlatarak başlar. Daha sonra tekrarlı olarak iki adım gerçekleştirir:
- her veri noktasını en yakın merkezoide atar, ve
- merkezoidleri her kümedeki tüm noktaların ortalaması olarak yeniden hesaplar.
Bu süreç, merkezoidler stabilize olana veya maksimum iterasyon sayısına ulaşılana kadar devam eder. K-means, küme içi kareler toplamını minimize etmeyi amaçlar, bu da kompakt ve belirgin kümeler oluşturur.
K-means kümeleme - interaktif demolar
Lütfen aşağıdaki siteleri ziyaret edin:
R ile K-means kümeleme
Kod için lütfen R ile K-means sayfasını ziyaret edin.
K-means kümelemenin avantajları
- Basitlik: Anlaşılması ve uygulanması kolay.
- Verimlilik: Genellikle hızlı ve hesaplama açısından verimli, özellikle büyük veri setleri için.
- Ölçeklenebilirlik: Yüksek boyutlu verilerle iyi çalışır.
- Esneklik: Uygun uzaklık metrikleriyle farklı veri türlerine uyarlanabilir.
- Yorumlanabilirlik: Sonuçta elde edilen kümeler genellikle yorumlanması kolaydır.
K-means kümelemenin dezavantajları
- Başlangıç merkezoidlerine duyarlılık: Sonuçlar, merkezoidlerin başlangıçtaki rastgele yerleşimine bağlı olarak değişebilir.
- Önceden tanımlanmış k gerektirir: Küme sayısı önceden belirtilmelidir, bu her zaman bilinmeyebilir.
- Küresel kümeler varsayar: Küresel olmayan küme şekilleriyle zayıf performans gösterir.
- Aykırı değerlere duyarlılık: Aykırı değerler, merkezoid hesaplamasını ve küme atamasını önemli ölçüde etkileyebilir.
- Değişen küme boyutlarıyla mücadele eder: Benzer mekansal büyüklükte kümeler oluşturma eğilimindedir.
- Yerel optima: Global optimum yerine yerel bir minimuma yakınsayabilir.
- Kategorik veriyi doğrudan işleyememe: Sayısal olmayan veriler için ön işleme gerektirir.
Hiyerarşik kümeleme
Hiyerarşik kümeleme, benzer veri noktalarını kümelere gruplandırmak için kullanılan denetimsiz bir makine öğrenimi tekniğidir. Önceden tanımlanmış bir küme sayısı gerektiren diğer kümeleme yöntemlerinin aksine, hiyerarşik kümeleme dendrogram adı verilen ağaç benzeri bir küme yapısı oluşturur. Bu yöntem, ya her veri noktasını kendi kümesi olarak başlatıp en yakın kümeleri iteratif olarak birleştirerek (birleştirici yaklaşım), ya da tüm veri noktalarını tek bir kümede başlatıp tekrarlı olarak bölerek (bölücü yaklaşım) çalışır. Bu süreç, istenen küme sayısı veya kümeler arası bir eşik mesafesi gibi bir durma kriteri karşılanana kadar devam eder.
Hiyerarşik kümeleme, verilerin doğal yapısını farklı detay seviyelerinde keşfetmek ve küme sayısının önceden bilinmediği veri setleri için özellikle kullanışlıdır.
Nasıl çalışır
Hiyerarşik kümeleme, seçilen bir uzaklık metriği (örn. Öklid uzaklığı) kullanarak tüm veri noktası çiftleri arasındaki uzaklıkları hesaplayarak başlar. Daha yaygın olan birleştirici yaklaşımda, her veri noktası kendi kümesi olarak başlar. Algoritma daha sonra bir bağlantı kriterine (örn. tek bağlantı, tam bağlantı veya ortalama bağlantı) göre en yakın iki kümeyi iteratif olarak birleştirir. Bu süreç, tüm veri noktaları tek bir kümede toplanana veya istenen küme sayısına ulaşılana kadar tekrarlanır, daha büyük kümeler oluşturur. Sonuç, bir dendrogram olarak görselleştirilebilen hiyerarşik bir yapıdır ve kullanıcıların ihtiyaçlarına en uygun kümeleme seviyesini seçmelerine olanak tanır.
Lütfen Veri Madenciliğinde Hiyerarşik Kümeleme ve Hiyerarşik Kümelemeye Giriş sayfalarını ziyaret edin.
Demolar için lütfen aşağıdaki siteyi ziyaret edin:
Hiyerarşik kümelemenin avantajları
Önceden tanımlanmış küme sayısı gerekmez: K-means’in aksine, hiyerarşik kümeleme önceden küme sayısının belirtilmesini gerektirmez.
Hiyerarşik temsil: Farklı seviyelerde veri yapısına dair içgörüler sunan bir dendrogram sağlar.
Küme detay seviyesinde esneklik: Kullanıcılar, dendrogramı farklı seviyelerden keserek ihtiyaçlarına en uygun kümeleme seviyesini seçebilirler.
Çeşitli veri türlerine uygulanabilirlik: Benzerlik veya uzaklık ölçüsü tanımlanabilen her veri türüne uygulanabilir.
Yorumlanabilirlik: Dendrogram, kümeleme sürecinin görsel olarak sezgisel bir temsilini sunar.
Farklı küme şekillerini işleyebilme: Sadece küresel olanlar değil, çeşitli şekil ve boyutlardaki kümeleri tanımlayabilir.
Dezavantajları
Hesaplama karmaşıklığı: Birçok uygulamada O(n^2) alan karmaşıklığı ve O(n^3) zaman karmaşıklığı, çok büyük veri setleri için daha az uygun hale getirir.
Gürültü ve aykırı değerlere duyarlılık: Aykırı değerler dendogramın şeklini önemli ölçüde etkileyebilir.
Yüksek boyutlu verileri ele almada zorluk: Boyut sayısı arttıkça performans ve yorumlanabilirlik azalabilir.
Geri alma eksikliği: Bir birleştirme veya bölme yapıldığında geri alınamaz, bu da optimal olmayan sonuçlara yol açabilir.
Bellek yoğun: Büyük veri setleri için uzaklık matrisini saklamak bellek yoğun olabilir.
Uzaklık metriği ve bağlantı yöntemi seçimi: Sonuçlar, seçilen uzaklık metriği ve bağlantı yöntemine göre önemli ölçüde değişebilir, dikkatli düşünme gerektirir.
Ölçeklenebilirlik sorunları: Çok büyük veri setleri için diğer bazı kümeleme yöntemlerine göre daha az ölçeklenebilir.
DBSCAN kümeleme
DBSCAN (Gürültülü Uygulamalarla Yoğunluk Tabanlı Mekansal Kümeleme), uzayda yakın paketlenmiş noktaları gruplandıran ve düşük yoğunluklu bölgelerde yalnız duran noktaları aykırı değer olarak işaretleyen popüler bir kümeleme algoritmasıdır.
Rastgele bir ziyaret edilmemiş nokta seçerek ve belirli bir yarıçap (ε) içindeki komşuluğunu keşfederek çalışır. Bu komşuluk minimum sayıda nokta (MinPts) içeriyorsa, bir küme oluşturulur. Algoritma daha sonra yeni eklenen noktaların komşuluklarını keşfederek kümeyi yinelemeli olarak genişletir. Bir nokta küme oluşturmak için yeterli komşuya sahip değilse, gürültü olarak etiketlenir. Bu süreç tüm noktalar ziyaret edilene kadar devam eder ve çeşitli şekil ve boyutlarda yoğun kümeler seti ile birlikte tanımlanmış gürültü noktaları ortaya çıkar.
İnteraktif demolar
Lütfen temel kavramlar hakkında DBSCAN — Görselleştirilmiş ve detaylı bir giriş sayfasını ziyaret edin.
DBSCAN algoritması için interaktif demo için lütfen DBSCAN Kümelemesini Görselleştirme sayfasını ziyaret edin.
DBSCAN Algoritması
DBSCAN’in Avantajları
- Şekil esnekliği: Sadece dairesel olanlar değil, keyfi şekilli kümeleri bulabilir.
- Aykırı değer tespiti: Otomatik olarak gürültü noktalarını ve aykırı değerleri tanımlar.
- Önceden tanımlanmış küme sayısı yok: K-means’in aksine, önceden küme sayısını belirtmeyi gerektirmez.
- Yoğunluk tabanlı: Farklı yoğunluktaki kümeleri ayırmada etkilidir.
- Sağlamlık: Merkez tabanlı algoritmalara göre aykırı değerlere daha az duyarlıdır.
Dezavantajları
- Parametre hassasiyeti: Sonuçlar, ε ve MinPts parametrelerinin seçimine bağlı olarak önemli ölçüde değişebilir.
- Değişen yoğunluklarla mücadele: Kümeler çok farklı yoğunluklara sahip olduğunda zorluk yaşayabilir.
- Yüksek boyutlu veriler: “Boyutsallık laneti” nedeniyle yüksek boyutlu uzaylarda performans ve etkinlik azalabilir.
- Bellek gereksinimleri: Büyük veri setleri için bellek yoğun olabilir.
- Ölçeklenebilirlik: Bazı diğer algoritmalara göre çok büyük veri setleri için o kadar verimli değildir.
- Bağlantı tabanlı: Kümelerin yakın ama seyrek alanlarla ayrıldığı veri setlerinde zorlanabilir.
Kümelemeyi değerlendirme
Tanım: Silhouette skoru -1 ile 1 arasında değişir, burada:
- 1’e yakın bir skor, veri noktasının kendi kümesine iyi uyduğunu ve komşu kümelere kötü uyduğunu gösterir.
- 0 civarında bir skor, veri noktasının iki komşu küme arasındaki karar sınırında veya çok yakınında olduğunu önerir.
- Negatif bir skor, veri noktasının yanlış kümeye atanmış olabileceğini gösterir.
Hesaplama: Her veri noktası i için, silhouette skoru s(i) şöyle hesaplanır:
s(i) = (b(i) - a(i)) / max(a(i), b(i))
Burada: a(i), i ile aynı kümedeki diğer tüm noktalar arasındaki ortalama mesafedir b(i), i ile i’nin parçası olmadığı en yakın kümedeki tüm noktalar arasındaki ortalama mesafedir
Yorumlama:
- Daha yüksek silhouette skorları daha iyi tanımlanmış kümeleri gösterir.
- Tüm noktalar üzerinden ortalama silhouette skoru, farklı kümeleme konfigürasyonlarını karşılaştırmak için kullanılabilir.
Sınıflandırma vs. Kümeleme
lütfen bu iki kavramı karşılaştırın