Sınıflandırma Yöntemleri
FEF3001 Yapay zekaya giriş - Ders5
2024-07-19
İçerik
- Denetimli öğrenmeye giriş
- Sınıflandırmanın tanımı ve uygulamaları
- Veri hazırlama
- Özellik seçimi ve ön işleme ✅
- Yöntemler
- Karar Ağaçları
- Rastgele Orman
- Destek Vektör Makineleri (SVM)
- Lojistik Regresyon
- K-en yakın komşu
- Naive Bayes
- Yapay Sinir Ağları ✅
- Ensemble yöntemleri
- Değerlendirme ✅
- Karmaşıklık Matrisi ✅
- Doğruluk, hassasiyet, geri çağırma, F1-skoru ✅
- ROC eğrileri ✅
- Aşırı öğrenme (overfitting) ve yetersiz öğrenme (underfitting) ✅
- Çapraz doğrulama (Cross Validation)
Denetimli Öğrenme
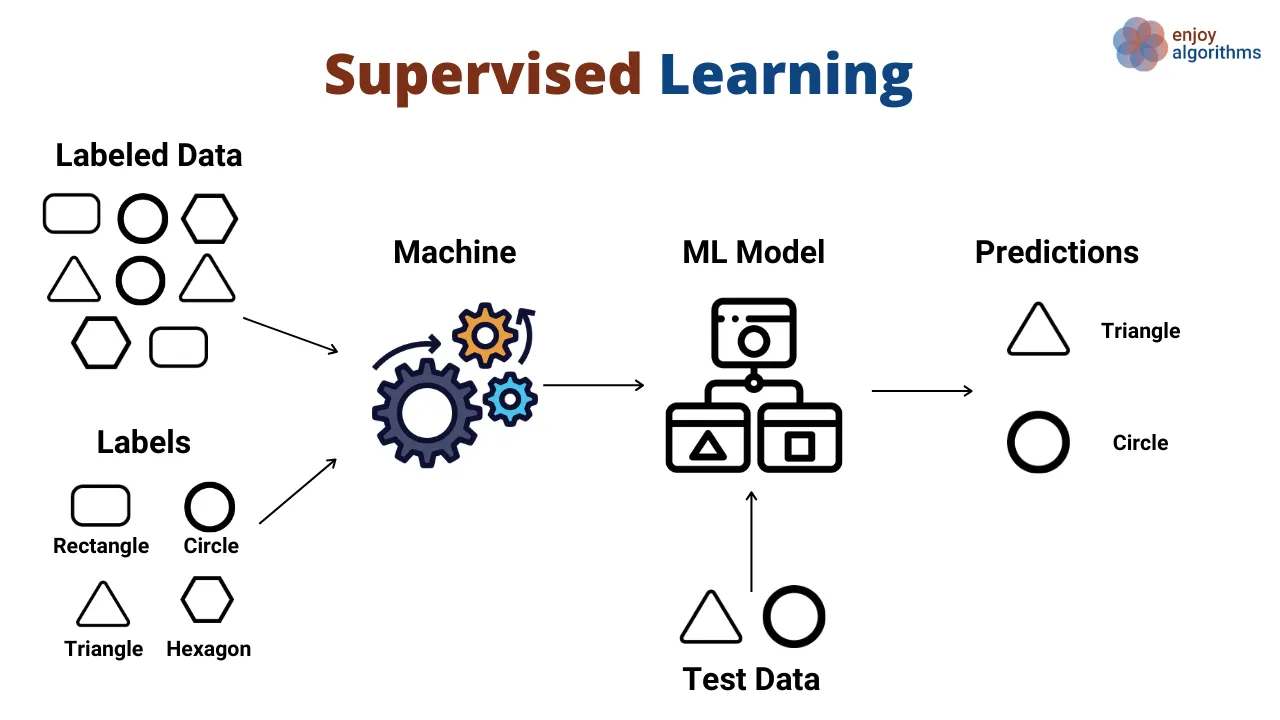
Denetimsiz Öğrenme
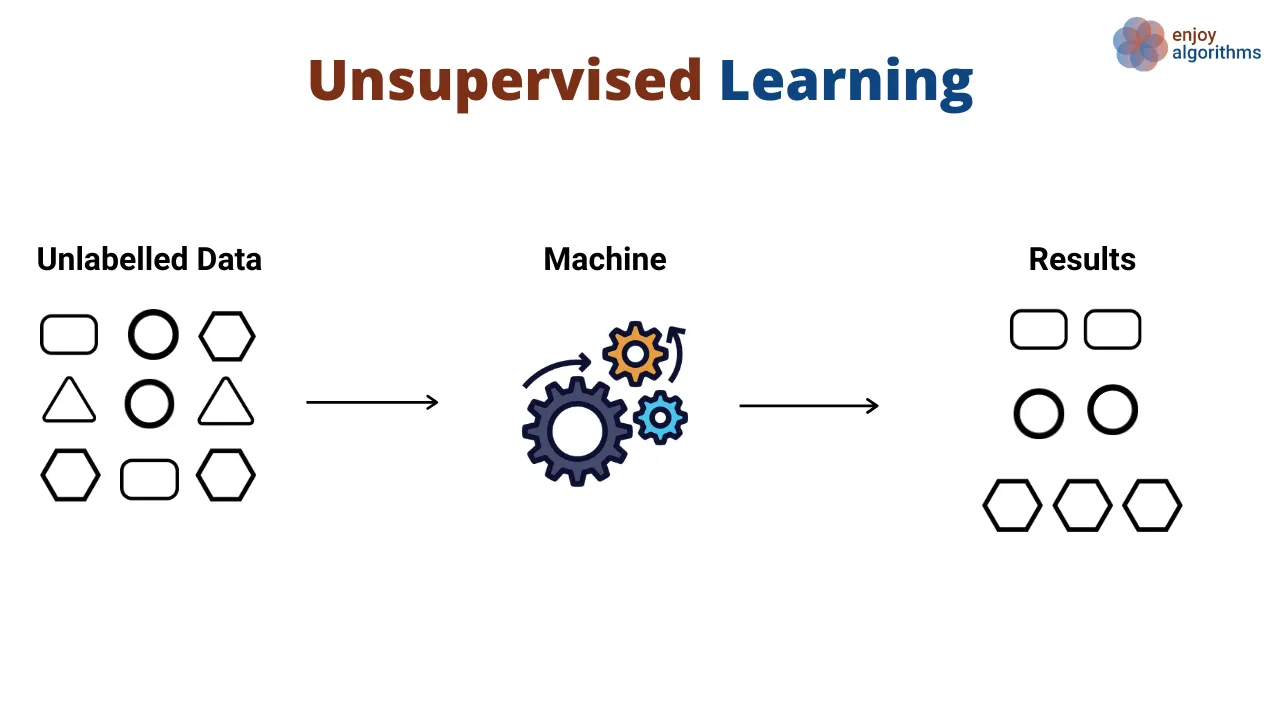
Sınıflandırmanın tanımı
- Denetimli öğrenmenin bir türü
- Amaç: Giriş verilerini önceden tanımlanmış sınıflara veya kategorilere ayırmak
- Model, sınıflar arasında karar sınırları çizmeyi öğrenir
- Çıktı, ayrık bir sınıf etiketidir (sürekli değerler tahmin eden regresyondan farklı olarak)
Uygulamalar
- Metin Sınıflandırma
- E-postalarda spam tespiti
- Ürün yorumlarının duygu analizi
- Haber makalelerinin kategorize edilmesi
- Görüntü Sınıflandırma
- Hastalık tespiti için tıbbi görüntüleme
- Yüz tanıma sistemleri
- Bitki veya hayvan türlerinin tanımlanması
- Finansal Uygulamalar
- Kredi puanlaması (kredi başvurularını onaylama/reddetme)
- İşlemlerde dolandırıcılık tespiti
- Sağlık Hizmetleri
- Belirtiler ve test sonuçlarına dayalı hastalık teşhisi
- Hasta yeniden yatış riskini tahmin etme
- Çevre Bilimi
- İklim deseni sınıflandırması
- Tür habitat tahmini
- Edebiyat ve Dilbilim
- Yazarlık atfı
- Metinlerin tür sınıflandırması
- Dil tanımlama
Sıra Sizde
Zoom sohbet penceresinde lütfen bölümünüzü ve alanınızla ilgili bir sınıflandırma görevi örneği yazın
Sıra Sizde
Bir örnek seçin ve veriler hakkında tartışın
Kaggle’ı ziyaret edin ve ilgili veri setini bulun
Karar Ağaçları
Karar Ağaçları, kararların ve olası sonuçlarının ağaç benzeri bir modelini kullanan bir sınıflandırma yöntemidir. Algoritma, veriyi özellik değerlerine göre bölen bir dizi eğer-o zaman-değilse karar kuralını öğrenir ve bir akış şemasına benzeyen bir yapı oluşturur. Her iç düğüm bir özellik üzerinde bir “test”i temsil eder, her dal testin sonucunu temsil eder ve her yaprak düğüm bir sınıf etiketi veya kararı temsil eder.
dal, test, yaprak
Örnek
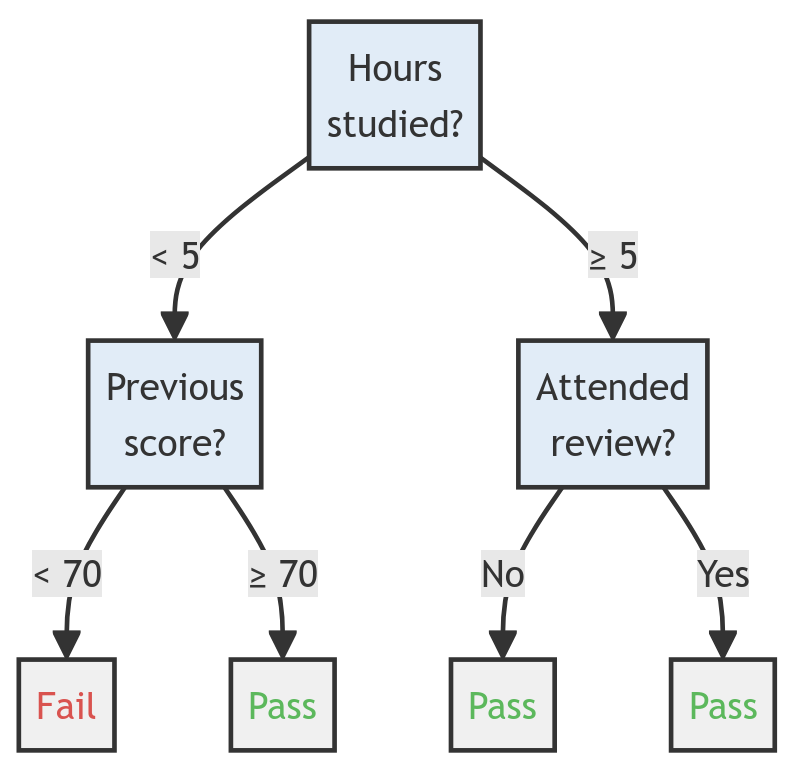
| Çalışılan saat | Önceki Puan | Uygulamaya Katıldı | Geçti? |
|---|---|---|---|
| 3 | 60 | Hayır | ? |
| 4 | 75 | Hayır | ? |
| 7 | 80 | Evet | ? |
Karar Ağacı Oluşturma için Temel Metrikler
Sorular: Hangi özellik ilk dal olur? Hangi değerde bir dal oluştururuz (5 saat, 70 puan, vb.)
- Entropi
- Bilgi Kazancı
- Gini Safsızlığı
Entropi
- Entropi, bir örnek kümesindeki safsızlık veya belirsizlik ölçüsüdür. Karar ağaçları bağlamında, bir veri kümesindeki sınıf etiketlerinin düzensizliğini ölçer.
Formül: \(H(S) = -\sum_{i=1}^{c} p_i \log_2(p_i)\)
Burada \(S\) veri kümesi, \(c\) sınıf sayısı ve \(p_i\), \(i\) sınıfına ait örneklerin oranıdır.
- 0 (tamamen saf, tüm örnekler bir sınıfa ait) ile \(\log_2(c)\) (tamamen saf olmayan, tüm sınıflara eşit dağılım) arasında değişir.
- Bilgi kazancını hesaplamak için kullanılır.
Bilgi Kazancı
- Bilgi kazancı, veriyi belirli bir özelliğe göre bölerek elde edilen entropi azalmasını ölçer. Karar ağacının her düğümünde hangi özelliğin bölünmesi gerektiğini belirlemeye yardımcı olur.
Formül: \(IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)\)
Burada \(S\) veri kümesi, \(A\) bölünme için düşünülen özellik, \(Values(A)\) \(A\) özelliğinin olası değerleri ve \(S_v\), \(A\) özelliğinin \(v\) değerine sahip olduğu \(S\)’nin alt kümesidir.
- Daha yüksek bilgi kazancı, sınıflandırma için daha faydalı bir özelliği gösterir.
- Genellikle her düğümde bölünme için en yüksek bilgi kazancına sahip özellik seçilir.
Gini Safsızlığı
- Gini safsızlığı, bir örnek kümesinin safsızlığını ölçmek için entropiye bir alternatiftir. Rastgele seçilen bir elemanın, alt kümedeki etiket dağılımına göre rastgele etiketlendirilirse yanlış sınıflandırılma olasılığını temsil eder.
Formül: \(Gini(S) = 1 - \sum_{i=1}^{c} (p_i)^2\)
Burada \(S\) veri kümesi, \(c\) sınıf sayısı ve \(p_i\), \(i\) sınıfına ait örneklerin oranıdır.
- 0 (tamamen saf) ile \(1 - \frac{1}{c}\) (tamamen saf olmayan) arasında değişir.
- Genellikle CART (Sınıflandırma ve Regresyon Ağaçları) gibi algoritmalarda kullanılır.
Entropi (bilgi kazancı ile) veya Gini safsızlığı kullanma seçimi genellikle karar ağacı algoritmasının belirli uygulamasına bağlıdır. Pratikte, genellikle benzer sonuçlar verirler.
Karar ağacı oluşturma algoritmaları
- ID3
- CART
Algoritmalar hakkında detaylar için lütfen bu bağlantıyı ziyaret edin
R ile bir örnek
https://www.dataspoof.info/post/decision-tree-classification-in-r/
https://forum.posit.co/t/decision-tree-in-r/5561/5
Karar Ağaçlarının Avantajları:
- Yorumlanabilirlik: Uzman olmayanlar için bile anlaşılması ve açıklanması kolaydır. Karar verme süreci görsel olarak temsil edilebilir.
- Az veya hiç veri ön işleme gerektirmez: Normalizasyon veya ölçeklendirme ihtiyacı olmadan hem sayısal hem de kategorik verileri işleyebilir.
- Hesaplama açısından verimli: Özellikle küçük ve orta ölçekli veri setleriyle eğitim ve tahmin yapmak genellikle hızlıdır.
Dezavantajları:
- Aşırı öğrenme: Özellikle derin ağaçlarda aşırı öğrenmeye eğilimlidir, bu da yeni verilerde zayıf genellemeye yol açar.
- İstikrarsızlık: Verideki küçük değişiklikler tamamen farklı bir ağacın oluşturulmasına neden olabilir.
- Yüksek boyutlu verilerle zorluk: Birçok özellikle hesaplama açısından pahalı hale gelebilir ve aşırı öğrenmeye eğilimli olabilir.
Quiz zamanı
Rastgele Orman (Random Forest)
Rastgele orman, Leo Breiman ve Adele Cutler tarafından tescillenen, birden çok karar ağacının çıktısını birleştirerek tek bir sonuca ulaşan yaygın olarak kullanılan bir makine öğrenimi algoritmasıdır.
Rastgele ormanlar, eğitim sırasında çok sayıda karar ağacı oluşturarak çalışan ve sınıflandırma, regresyon ve diğer görevler için kullanılan bir topluluk öğrenme yöntemidir. Sınıflandırma görevleri için rastgele ormanın çıktısı, çoğu ağaç tarafından seçilen sınıftır.
Kaggle örneği
Lütfen şu adresi ziyaret edin: https://www.kaggle.com/code/lara311/diabetes-prediction-using-machine-learning
Destek Vektör Makineleri
Temel Fikir
Farklı türdeki nesneleri, örneğin elmaları ve portakalları, renk, şekil ve boyut gibi özelliklerine göre ayırmaya çalıştığınızı hayal edin. İki tür nesneyi mümkün olduğunca doğru bir şekilde ayıran bir çizgi (veya daha yüksek boyutlarda bir hiper düzlem) çizmek istiyorsunuz.
Destek Vektör Makineleri = Support Vector Machines (SVM)
SVM Yöntemi
Destek Vektör Makinesi, veriyi farklı sınıflara ayıran en iyi hiper düzlemi bulmayı amaçlayan bir tür denetimli öğrenme algoritmasıdır. İşte nasıl çalıştığı:
- Veri Hazırlama: İlgili özellikleri (öznitelikleri) ve etiketleri (örneğin, “elma” veya “portakal”) olan nesnelerin (örneğin, elmalar ve portakallar) bir veri setini toplayın.
- Verileri Çizme: Veri noktalarını bir özellik uzayında çizin, burada her eksen bir özelliği (örneğin, renk, şekil, boyut) temsil eder.
- Hiperdüzlemi Bulma: Amaç, veri noktalarını farklı sınıflara ayıran bir hiperdüzlem bulmaktır. Hiperdüzlem, özellik uzayını iki bölgeye ayıran bir çizgi (2B’de) veya düzlem (3B’de) dir.
- Marjini Maksimize Etme: SVM algoritması, iki sınıf arasındaki marjini maksimize eden hiperdüzlemi bulmaya çalışır. Marj, hiperdüzlem ile hiperdüzlemin her iki tarafındaki en yakın veri noktaları (destek vektörleri olarak adlandırılır) arasındaki mesafedir.
- Destek Vektörleri: Destek vektörleri, hiperdüzleme en yakın olan ve konumu üzerinde en çok etkiye sahip olan veri noktalarıdır. Bunlar, hiperdüzlemi tanımlamaya yardımcı olan “destekler”dir.
Destek Vektör Makineleri
Temel Kavramlar
- Hiperdüzlem: Verileri farklı sınıflara ayıran bir çizgi (2B’de) veya düzlem (3B’de).
- Marj: Hiperdüzlem ile hiperdüzlemin her iki tarafındaki en yakın veri noktaları (destek vektörleri) arasındaki mesafe.
- Destek Vektörleri: Hiperdüzleme en yakın olan ve konumu üzerinde en çok etkiye sahip olan veri noktaları.
SVM’ler Neden Faydalıdır
SVM’ler güçlüdür çünkü:
- Yüksek boyutlu verileri işleyebilirler
- Gürültüye ve aykırı değerlere karşı dayanıklıdırlar
- Hem sınıflandırma hem de regresyon görevleri için kullanılabilirler
- Karar sınırının net bir geometrik yorumunu sağlarlar
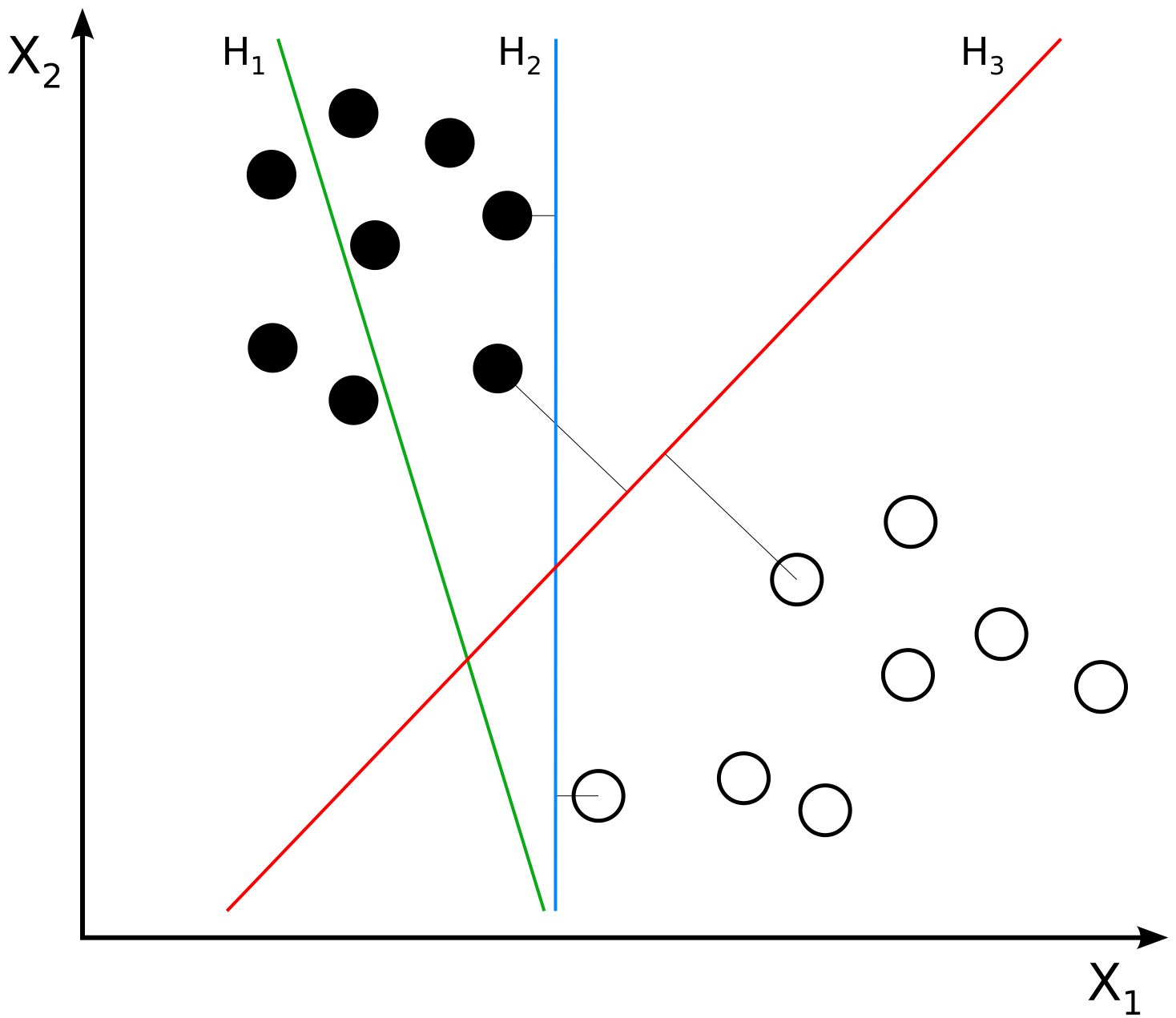
H1 sınıfları ayırmaz. H2 ayırır, ancak sadece küçük bir marjla. H3 onları maksimum marjla ayırır. Kaynak
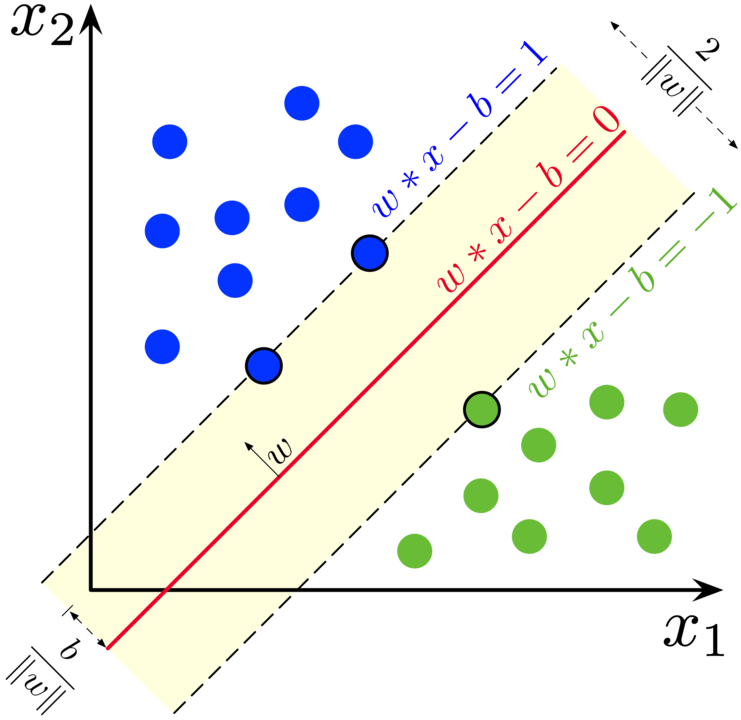
İki sınıftan örneklerle eğitilmiş bir SVM için maksimum marjlı hiperdüzlem ve marjlar. Marj üzerindeki örneklere destek vektörleri denir. Kaynak
SVM için çevrimiçi interaktif bir demo için lütfen SVM demo sitesini ziyaret edin.
Lojistik Regresyon
Temel Fikir
Lojistik regresyon, bir sonucun, olayın veya gözlemin olasılığını tahmin ederek ikili sınıflandırma görevlerini gerçekleştiren denetimli bir makine öğrenimi algoritmasıdır. Model, iki olası sonuçla sınırlı ikili bir sonuç sunar: evet/hayır, 0/1 veya doğru/yanlış.
Lojistik Regresyon Yöntemi
Lojistik Regresyon, bir dizi girdi değişkenine (örneğin, puanlar) dayalı olarak bir olayın gerçekleşme olasılığını (örneğin, sınavı geçme) modelleyen bir tür denetimli öğrenme algoritmasıdır. İşte nasıl çalıştığı:
- Veri Hazırlama: Girdi değişkenleri (örneğin, puanlar) ve çıktı değişkenleri (örneğin, geçti/kaldı) için bir veri seti toplayın.
- Lojistik Fonksiyon: Lojistik fonksiyon, aynı zamanda sigmoid fonksiyonu olarak da bilinen, olayın gerçekleşme olasılığını modellemek için kullanılır. Girdi değişkenlerini 0 ile 1 arasında bir olasılığa eşler.
- Log-Odds: Lojistik fonksiyon, olayın gerçekleşme olasılığının log-odds’una dayanır, bu da olayın gerçekleşme olasılığının olayın gerçekleşmeme olasılığına oranının logaritmasıdır.
- Katsayılar: Algoritma, her girdi değişkeni için katsayıları (ağırlıkları) öğrenir, bu da her değişkenin çıktıyı tahmin etmedeki önemini belirler.
- Karar Sınırı: Algoritma, katsayıları ve lojistik fonksiyonu kullanarak bir karar sınırı oluşturur, bu da girdi uzayını iki bölgeye ayırır: her sınıf için bir tane (örneğin, geçti ve kaldı).
- Tahmin: Yeni bir girdi için, algoritma lojistik fonksiyonu ve öğrenilen katsayıları kullanarak olayın gerçekleşme olasılığını hesaplar. Eğer olasılık belirli bir eşiğin üzerindeyse (örneğin, 0.5), algoritma olayın gerçekleşeceğini tahmin eder (örneğin, öğrenci geçecek).
Temel Kavramlar
- Lojistik Fonksiyon: Girdi değişkenlerini 0 ile 1 arasında bir olasılığa eşleyen matematiksel bir fonksiyon.
- Log-Odds: Olayın gerçekleşme olasılığının olayın gerçekleşmeme olasılığına oranının logaritması.
- Katsayılar: Algoritmanın her girdi değişkeni için öğrendiği ağırlıklar, bunlar çıktıyı tahmin etmedeki önemlerini belirler.
- Karar Sınırı: Girdi uzayını iki bölgeye ayıran sınır, her sınıf için bir tane.
Lojistik Regresyon Neden Faydalıdır
Lojistik Regresyon popüler bir algoritmadır çünkü:
- Uygulaması ve yorumlanması kolaydır
- Birden çok girdi değişkenini işleyebilir
- Her tahmin için bir olasılık tahmini sağlar
- Tıp, finans ve pazarlama gibi birçok alanda yaygın olarak kullanılır