Ders 9: Hesapsal İstatistik

MBG1032 Biyoistatistik - Doç.Dr.Alper YILMAZ - 12 Mayıs 2025

Özet

Çok çekirdek - simulasyon
Hesapsal istatistik - “Allen Downey - A future of data science” başlıklı konuşması
R/infer paketi

Hesapsal istatistik

“A future of data science” başlıklı konuşmadan alınmıştır

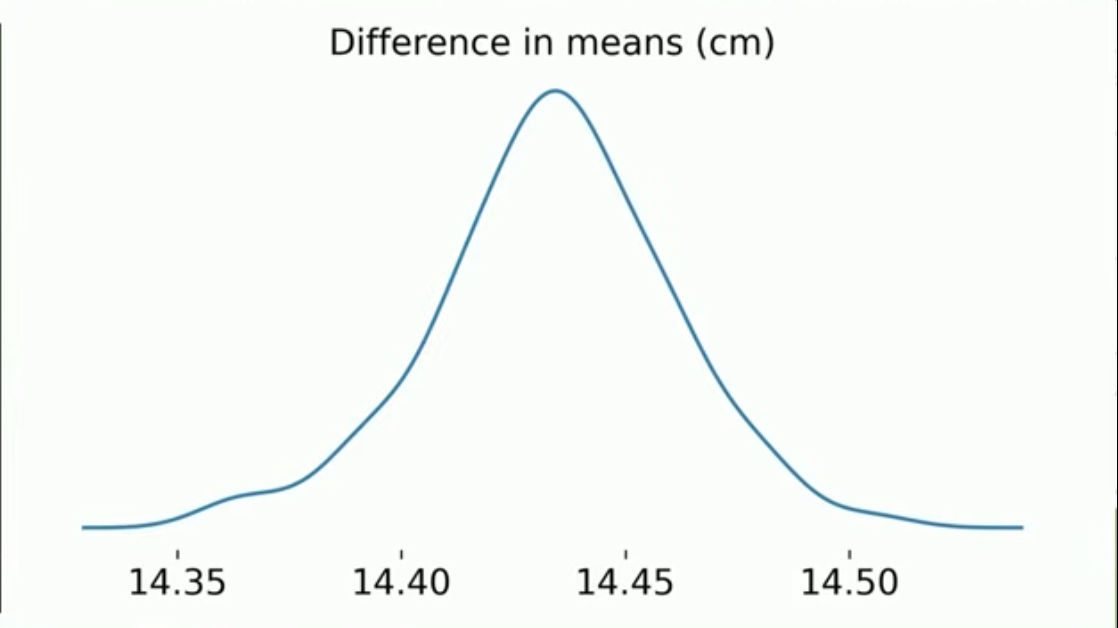
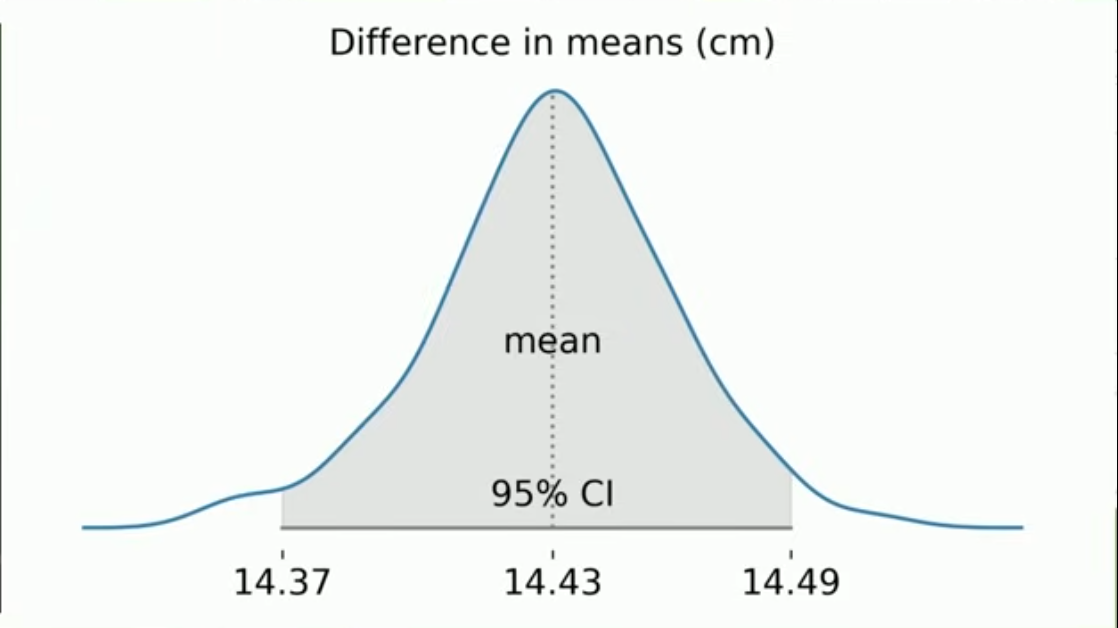
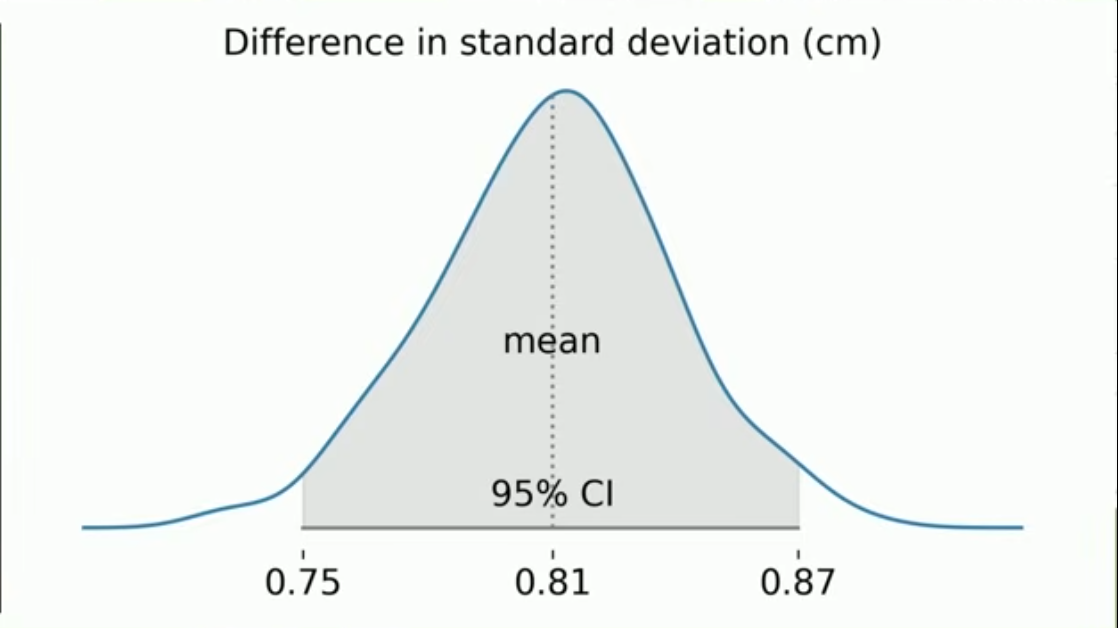
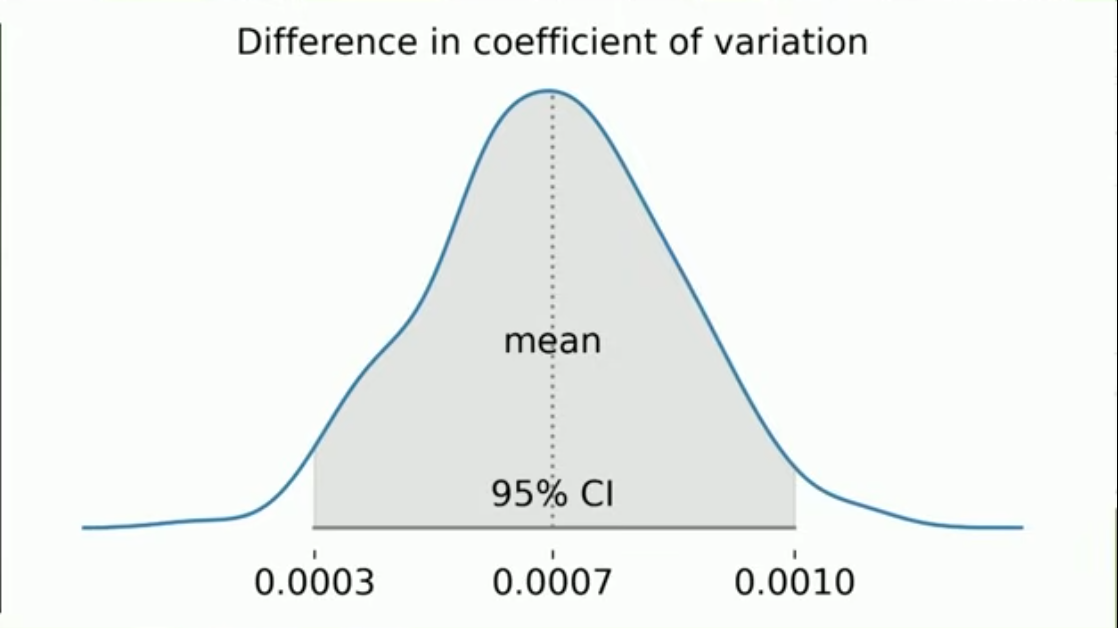
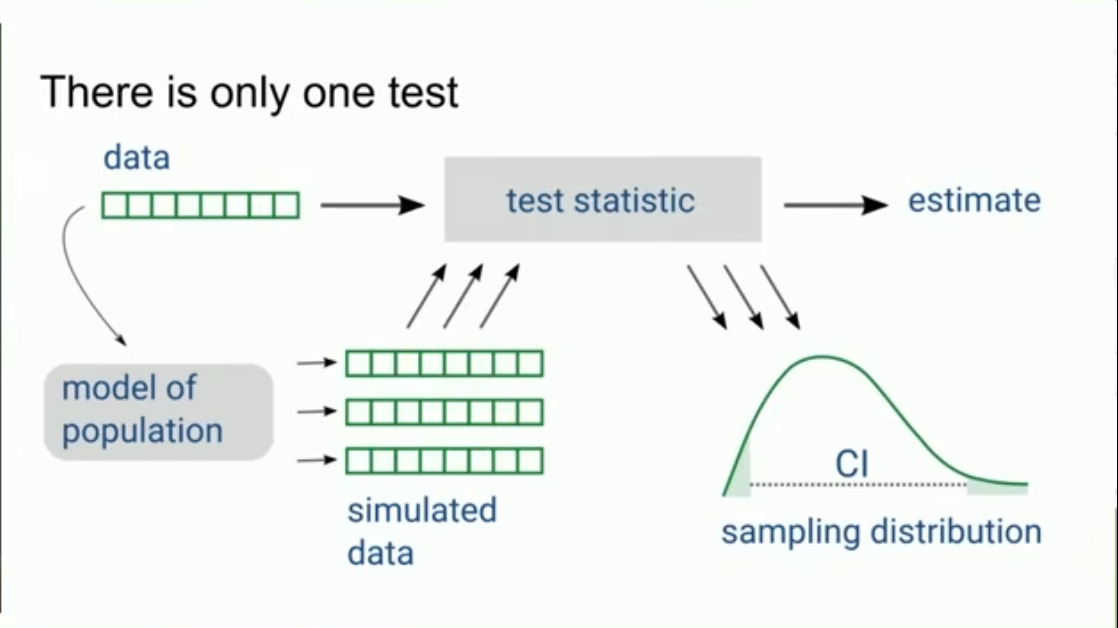
Geleneksel İstatistikten Simülasyona

Şimdiye kadar t-test, ANOVA ve Ki-kare gibi parametrik testleri öğrendik
Bu testler belirli varsayımlara dayanır (normallik, varyans homojenliği vb.)
Bugün farklı bir bakış açısı ile tanışacağız
Soru aynı: “Gözlediğimiz etki gerçek mi, yoksa şansa bağlı mı?”

Simülasyon Tabanlı İstatistik

Modern bilgisayarların gücünü kullanarak veri yeniden örnekleme
Rastgele süreçleri taklit etme
Teorik dağılımlar yerine veriden öğrenme
R’daki infer paketi bu yaklaşımı kolaylaştırır

infer Paketi Nedir?

İstatistiksel çıkarım için tutarlı bir dilbilgisi sağlar
tidyverse felsefesiyle uyumlu
Karmaşık formüller yerine okunabilir kod akışı
Dört ana fonksiyon: specify(), hypothesize(), generate(), calculate()

infer İş Akışı

İnfer Paketi İş Akışı

Örnek Veri Seti: GSS

library(infer)
library(dplyr)
data(gss)
glimpse(gss)

Rows: 500
Columns: 11
$ year    <dbl> 2014, 1994, 1998, 1996, 1994, 1996, 1990, 2016, 2000, 1998, 20…
$ age     <dbl> 36, 34, 24, 42, 31, 32, 48, 36, 30, 33, 21, 30, 38, 49, 25, 56…
$ sex     <fct> male, female, male, male, male, female, female, female, female…
$ college <fct> degree, no degree, degree, no degree, degree, no degree, no de…
$ partyid <fct> ind, rep, ind, ind, rep, rep, dem, ind, rep, dem, dem, ind, de…
$ hompop  <dbl> 3, 4, 1, 4, 2, 4, 2, 1, 5, 2, 4, 3, 4, 4, 2, 2, 3, 2, 1, 2, 5,…
$ hours   <dbl> 50, 31, 40, 40, 40, 53, 32, 20, 40, 40, 23, 52, 38, 72, 48, 40…
$ income  <ord> $25000 or more, $20000 - 24999, $25000 or more, $25000 or more…
$ class   <fct> middle class, working class, working class, working class, mid…
$ finrela <fct> below average, below average, below average, above average, ab…
$ weight  <dbl> 0.8960034, 1.0825000, 0.5501000, 1.0864000, 1.0825000, 1.08640…

1. `specify()`: Değişkenleri Belirleme

Hangi değişkenler üzerinde çalışacağımızı belirteriz
Tek değişken için: response = degisken
İki değişken için: response = y, explanatory = x veya y ~ x

# Yaş değişkenini belirtelim
gss |>
  specify(response = age)

Response: age (numeric)
# A tibble: 500 × 1
     age
   <dbl>
 1    36
 2    34
 3    24
 4    42
 5    31
 6    32
 7    48
 8    36
 9    30
10    33
# ℹ 490 more rows

# İki değişken ilişkisini belirtelim
gss |>
  specify(age ~ partyid)

Response: age (numeric)
Explanatory: partyid (factor)
# A tibble: 500 × 2
     age partyid
   <dbl> <fct>  
 1    36 ind    
 2    34 rep    
 3    24 ind    
 4    42 ind    
 5    31 rep    
 6    32 rep    
 7    48 dem    
 8    36 ind    
 9    30 rep    
10    33 dem    
# ℹ 490 more rows

2. `hypothesize()`: Sıfır Hipotezini Belirleme

İki temel sıfır hipotezi türü:
- "independence": İki değişken arasında ilişki yok
- "point": Parametre belirli bir değere eşit

# Bağımsızlık hipotezi
gss |>
  specify(college ~ partyid, success = "degree") |>
  hypothesize(null = "independence")

Response: college (factor)
Explanatory: partyid (factor)
Null Hypothesis: independence
# A tibble: 500 × 2
   college   partyid
   <fct>     <fct>  
 1 degree    ind    
 2 no degree rep    
 3 degree    ind    
 4 no degree ind    
 5 degree    rep    
 6 no degree rep    
 7 no degree dem    
 8 degree    ind    
 9 degree    rep    
10 no degree dem    
# ℹ 490 more rows

# Ortalama için nokta hipotezi
gss |>
  specify(response = hours) |>
  hypothesize(null = "point", mu = 40)

Response: hours (numeric)
Null Hypothesis: point
# A tibble: 500 × 1
   hours
   <dbl>
 1    50
 2    31
 3    40
 4    40
 5    40
 6    53
 7    32
 8    20
 9    40
10    40
# ℹ 490 more rows

3. `generate()`: Sıfır Dağılımı Oluşturma

Sıfır hipotezi altında verinin nasıl görüneceğini simüle eder
Üç temel yöntem:
- bootstrap: Yerine koyarak örnekleme
- permute: Değişkenleri karıştırma
- draw: Teorik dağılımdan örnekleme

# 1000 bootstrap örneği oluşturalım
gss |>
  specify(response = hours) |>
  hypothesize(null = "point", mu = 40) |>
  generate(reps = 1000, type = "bootstrap")

Response: hours (numeric)
Null Hypothesis: point
# A tibble: 500,000 × 2
# Groups:   replicate [1,000]
   replicate hours
       <int> <dbl>
 1         1  38.6
 2         1  55.6
 3         1  38.6
 4         1  50.6
 5         1  38.6
 6         1  18.6
 7         1  23.6
 8         1  18.6
 9         1  38.6
10         1  58.6
# ℹ 499,990 more rows

`generate()`: Veri Karıştırma Örneği

# Yaş ve parti ilişkisini kırmak için değişkenleri karıştıralım
gss |>
  specify(partyid ~ age) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute")

Response: partyid (factor)
Explanatory: age (numeric)
Null Hypothesis: independence
# A tibble: 500,000 × 3
# Groups:   replicate [1,000]
   partyid   age replicate
   <fct>   <dbl>     <int>
 1 ind        36         1
 2 ind        34         1
 3 rep        24         1
 4 dem        42         1
 5 dem        31         1
 6 rep        32         1
 7 ind        48         1
 8 rep        36         1
 9 dem        30         1
10 rep        33         1
# ℹ 499,990 more rows

Bu adım, sıfır hipotezi doğru olsaydı veri nasıl görünürdü sorusuna cevap verir.

4. `calculate()`: İstatistik Hesaplama

Simüle edilmiş verilerden istatistikler hesaplar
Ortalama, medyan, oran, fark, t-istatistiği ve daha fazlası
Sıfır dağılımını oluşturur

# Ortalama çalışma saatlerinin dağılımını hesaplayalım
gss |>
  specify(response = hours) |>
  hypothesize(null = "point", mu = 40) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

Response: hours (numeric)
Null Hypothesis: point
# A tibble: 1,000 × 2
   replicate  stat
       <int> <dbl>
 1         1  40.5
 2         2  40.6
 3         3  39.3
 4         4  39.7
 5         5  40.0
 6         6  39.9
 7         7  39.7
 8         8  40.8
 9         9  40.3
10        10  40.6
# ℹ 990 more rows

Örnek: Haftalık Çalışma Saatleri Analizi

Soru: Ortalama çalışma saati gerçekten 40 saat mı?

# Gözlemlenen istatistiği hesaplayalım
obs_mean <- gss |>
  specify(response = hours) |>
  calculate(stat = "mean")

# Sıfır dağılımını oluşturalım
null_dist <- gss |>
  specify(response = hours) |>
  hypothesize(null = "point", mu = 40) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

Sonuçları Görselleştirme

# Sıfır dağılımını görselleştirelim
null_dist |>
  visualize() +
  shade_p_value(obs_stat = obs_mean, direction = "two-sided")

p-değeri Hesaplama

# İki kuyruklu p-değerini hesaplayalım
p_value <- null_dist |>
  get_p_value(obs_stat = obs_mean, direction = "two-sided")

p_value

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.032

Eğer ortalama gerçekten 40 saat olsaydı, gözlemlediğimiz kadar (veya daha) uç bir değer elde etme olasılığımız p-değeri kadardır.

Güven Aralıkları

# Bootstrap dağılımını oluşturalım
boot_dist <- gss |>
  specify(response = hours) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

# %95 güven aralığını hesaplayalım
ci <- boot_dist |>
  get_confidence_interval(
    point_estimate = obs_mean,
    level = .95,
    type = "se"
  )

Moleküler Biyoloji Örneği: Gen İfadesi

Senaryo: İki farklı hücre tipinde (normal vs. kanser) bir genin ifade seviyesini karşılaştırıyoruz
Sıfır hipotezi: Gen ifadesi hücre tipine göre değişmez
infer ile simülasyon yaklaşımı nasıl kullanılır?

Örnek Kod: Gen İfadesi Karşılaştırması

# Verileri tanımlayalım
gen_ifadesi |>
  # İfade seviyesi ~ hücre tipi ilişkisini belirtelim
  specify(expression ~ cell_type) |>
  # Sıfır hipotezi: Hücre tipi etkisi yok
  hypothesize(null = "independence") |>
  # 1000 permütasyon örneği oluşturalım
  generate(reps = 1000, type = "permute") |>
  # Ortalama farkını hesaplayalım
  calculate(stat = "diff in means", 
            order = c("cancer", "normal"))

Teorik Dağılım Kullanımı

infer teorik dağılımlarla da çalışabilir
t, F, Ki-kare ve z dağılımları için assume()
Simülasyon ve teorik yaklaşımlar arasında geçiş yapabilirsiniz

# t-dağılımı tanımlayalım
t_dist <- gen_ifadesi |>
  specify(expression ~ cell_type) |>
  assume(distribution = "t")

infer’in Avantajları

Daha anlaşılır istatistiksel süreç
Varsayımlar konusunda daha esnek
Öğrencilere istatistiği görselleştirme imkanı
Tidyverse ekosistemiyle entegrasyon
Karmaşık analizleri basitleştirme