Ders 8: Ki-kare Testi
MBG1032 Biyoistatistik - Doç.Dr.Alper YILMAZ - 5 Mayıs 2025
Özet
- Ki-kare (χ²) testi nedir ve ne zaman kullanılır?
- Ki-kare dağılımı
- Ki-kare uygunluk testi (Goodness of Fit)
- Ki-kare bağımsızlık testi (Test of Independence)
- Ki-kare homojenlik testi (Test of Homogeneity)
- Mendel’in çalışmaları ve Ki-kare testi
- Ki-kare testinin varsayımları
- R ile Ki-kare uygulamaları
- Ki-kare sonuçlarının yorumlanması ve raporlanması
- Biyolojide Ki-kare uygulama örnekleri
Ki-kare (χ²) Testi Nedir?
Ki-kare testi, kategorik değişkenler için kullanılan parametrik olmayan bir istatistiksel testtir.
Temel Amaç:
- Gözlenen frekansların beklenen frekanslardan farklı olup olmadığını test etmek
- Kategorik değişkenler arasında ilişki olup olmadığını incelemek
Kullanım Alanları:
- Genetik çalışmalarda (alellik dağılımı, kalıtım paterni)
- Epidemiyolojik araştırmalarda (hastalık-risk faktörü ilişkisi)
- Sosyolojik çalışmalarda (anket verileri analizi)
- Ekolojik çalışmalarda (türlerin habitat tercihleri)
Ki-kare (χ²) Dağılımı
Ki-kare dağılımı, bağımsız standart normal dağılmış değişkenlerin karelerinin toplamının dağılımıdır.
Özellikleri:
- Sürekli bir dağılımdır
- Sadece pozitif değerler alır (χ² ≥ 0)
- Sağa çarpıktır (sağa kuyruklu)
- Serbestlik derecesi (df) arttıkça normale yaklaşır
- Tek parametreli bir dağılımdır: serbestlik derecesi (df)
Matematiksel İfade:
\(\chi^2 = \sum_{i=1}^{k} Z_i^2\)
Burada \(Z_i\)’ler bağımsız standart normal değişkenlerdir.

Ki-kare Dağılımları
Görsel Kaynak: Wikimedia Commons
Ki-kare Testleri Türleri
Ki-kare testi, farklı amaçlar için kullanılabilir:
- Ki-kare Uygunluk Testi (Goodness of Fit):
- Tek bir kategorik değişkenin gözlenen dağılımının, teorik veya beklenen bir dağılıma uyup uymadığını test eder.
- Örnek: Mendel’in bezelye deneylerinde gözlenen fenotip oranlarının 3:1 teorik oranına uyup uymadığını test etmek.
- Ki-kare Bağımsızlık Testi (Independence Test):
- İki kategorik değişken arasında ilişki olup olmadığını test eder.
- Örnek: Cinsiyet ile belirli bir genetik hastalığın görülme sıklığı arasında ilişki olup olmadığını test etmek.
- Ki-kare Homojenlik Testi (Homogeneity Test):
- Farklı popülasyonların bir kategorik değişken bakımından benzer dağılımlara sahip olup olmadığını test eder.
- Örnek: Farklı coğrafi bölgelerdeki kan grubu dağılımlarının benzer olup olmadığını test etmek.
Ki-kare Uygunluk Testi
Amaç: Gözlenen frekansların teorik/beklenen bir dağılıma uygunluğunu test etmek.
Hipotezler:
- H₀: Gözlenen frekanslar, beklenen dağılıma uygundur.
- H₁: Gözlenen frekanslar, beklenen dağılımdan farklıdır.
Test İstatistiği: \(\chi^2 = \sum_{i=1}^{k} \frac{(O_i - E_i)^2}{E_i}\)
Burada:
- \(O_i\) = i. kategorideki gözlenen frekans
- \(E_i\) = i. kategorideki beklenen frekans
- \(k\) = kategori sayısı
Serbestlik Derecesi: df = k - 1 - m
- \(k\) = kategori sayısı
- \(m\) = tahmin edilen parametre sayısı
Mendel ve Ki-kare Testi
Gregor Mendel (1822-1884), modern genetiğin babası olarak kabul edilir. Bezelye bitkilerinde yaptığı deneyler ile kalıtım yasalarını keşfetmiştir.
Mendel’in Çalışmaları:
- Yaptığı deneylerde, çeşitli özelliklerin (boy, çiçek rengi, tohum şekli) kalıtım paternlerini inceledi
- Dominant ve resesif alelleri tanımladı
- Monohybrid çaprazlamalarında 3:1 oranını gözlemledi (dominant:resesif)
- Dihybrid çaprazlamalarında 9:3:3:1 oranını gözlemledi
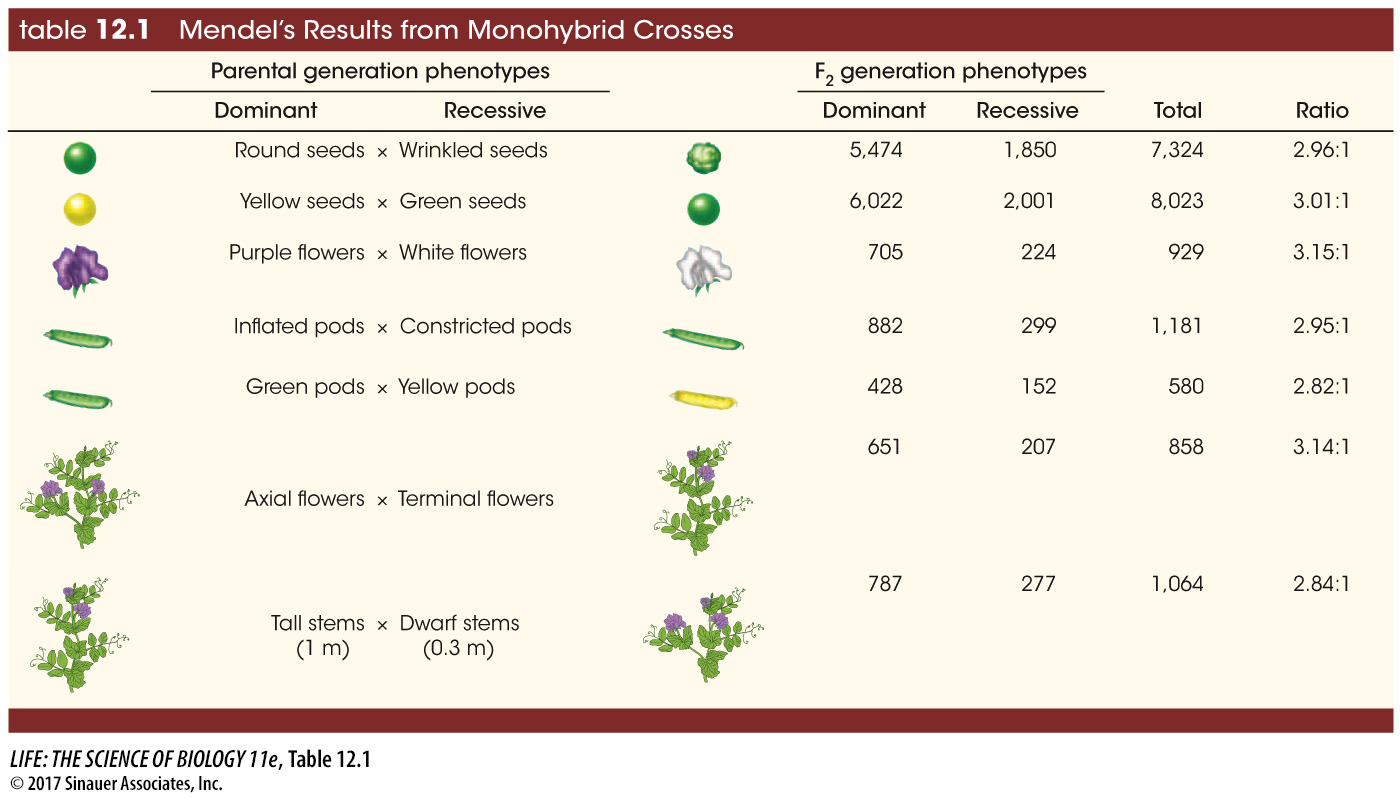
Mendel’in Monohybrid Çaprazlaması ve Ki-kare Analizi
Senaryo: Mendel’in sarı (dominant, Y) x yeşil (resesif, y) bezelye tohumu çaprazlamasından sonra F2 nesilde gözlenen fenotipik oranları inceleyelim.
Mendel’in Teorik Beklentisi: 3:1 oranı (3 sarı : 1 yeşil)
Ki-kare ile ilgili R fonksiyonları
- dchisq() - Ki-kare olasılık yoğunluk fonksiyonu (probability density function)
- Kullanım: dchisq(x, df) - belirli bir x değeri için olasılık yoğunluğunu hesaplar
- Örnek: dchisq(5, df=3) - 3 serbestlik derecesinde x=5 için olasılık yoğunluğu
- pchisq() - Ki-kare birikimli dağılım fonksiyonu (cumulative distribution function)
- Kullanım: pchisq(q, df, lower.tail=TRUE) - q değerinden küçük veya eşit değerlerin olasılığı
- Örnek: pchisq(7.81, df=3) - 3 serbestlik derecesinde 7.81’den küçük veya eşit değerlerin olasılığı
- p-değerini bulmak için: pchisq(q, df, lower.tail=FALSE) - q değerinden büyük değerlerin olasılığı
- qchisq() - Ki-kare dağılımının kantil fonksiyonu (quantile function)
- Kullanım: qchisq(p, df, lower.tail=TRUE) - belirli bir olasılık değerine karşılık gelen Ki-kare değeri
- Örnek: qchisq(0.95, df=3) - 3 serbestlik derecesinde %95’lik kantil değeri
- rchisq() - Ki-kare dağılımından rastgele sayılar üretme
- Kullanım: rchisq(n, df) - belirli bir serbestlik derecesi için n adet rastgele Ki-kare değeri
- Örnek: rchisq(100, df=3) - 3 serbestlik derecesinde 100 rastgele değer
- chisq.test() - Ki-kare testi yapma
- Uygunluk testi için: chisq.test(x, p=NULL) - x vektörü ve beklenen olasılıklar
- Bağımsızlık testi için: chisq.test(tablo) - iki yönlü kontenjans tablosu
- Örnek: chisq.test(c(89, 37, 30), p=c(0.6, 0.2, 0.2))
R ile Ki-kare Uygunluk Testi
Mendel’in verilerini R’ın chisq.test() fonksiyonu ile analiz edelim:
Mendel’in Dihybrid Çaprazlaması
Senaryo: Mendel’in sarı-düzgün (YYRR) x yeşil-buruşuk (yyrr) bezelye tohumu çaprazlamasından sonra F2 nesilde gözlenen fenotipik oranları inceleyelim.
Mendel’in Teorik Beklentisi: 9:3:3:1 oranı
- 9/16 Sarı-Düzgün (Y-R-)
- 3/16 Sarı-Buruşuk (Y-rr)
- 3/16 Yeşil-Düzgün (yyR-)
- 1/16 Yeşil-Buruşuk (yyrr)
Ki-kare tablosu
Ki-kare Bağımsızlık Testi
Amaç: İki kategorik değişken arasında anlamlı bir ilişki olup olmadığını test etmek.
Hipotezler:
- H₀: İki değişken birbirinden bağımsızdır (ilişki yoktur).
- H₁: İki değişken arasında bir ilişki vardır (bağımlıdır).
Test İstatistiği: \(\chi^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\)
Burada:
- \(O_{ij}\) = i. satır, j. sütundaki gözlenen frekans
- \(E_{ij}\) = i. satır, j. sütundaki beklenen frekans
- \(r\) = satır sayısı, \(c\) = sütun sayısı
Serbestlik Derecesi: df = (r - 1) × (c - 1)
Beklenen Frekansların Hesaplanması:
\(E_{ij} = \frac{(\text{i. satır toplamı}) \times (\text{j. sütun toplamı})}{\text{genel toplam}}\)
Örnek Ki-kare Bağımsızlık Testi: Kan Grubu ve Hastalık İlişkisi
Senaryo: Bir hastalığın görülme sıklığı ile kan grupları arasında bir ilişki olup olmadığını test etmek istiyoruz.
Görselleştirme
Bağımsızlık Testi Yorumlanması
p-değeri < 0.05 ise, iki değişken arasında anlamlı bir ilişki olduğu sonucuna varırız (H₀ reddedilir).
Ki-kare Testinin Varsayımları
Ki-kare testi, parametrik olmayan bir test olmasına rağmen, bazı varsayımlara dayanır:
Bağımsızlık: Gözlemler birbirinden bağımsız olmalıdır.
Rastgele Örnekleme: Veriler popülasyondan rastgele seçilmelidir.
Kategorik Veri: Ki-kare testi yalnızca kategorik (nominal veya ordinal) verilere uygulanabilir.
Yeterli Örnek Boyutu: Beklenen frekansların çoğu 5’ten büyük olmalıdır. Genellikle, beklenen frekansların en fazla %20’si 5’ten küçük olabilir ve hiçbir beklenen frekans 1’den küçük olmamalıdır.
Varsayımlar Karşılanmadığında:
- Fisher’ın Kesin Testi (küçük örneklemler için)
- Kategorileri birleştirerek beklenen frekansları artırmak
Fisher’ın Kesin Testi
Fisher’ın Kesin Testi, özellikle örneklem boyutu küçük olduğunda ve Ki-kare testinin varsayımları karşılanmadığında kullanılabilir.
Biyolojide Ki-kare Uygulamaları
Ki-kare testi, biyoloji alanında yaygın olarak kullanılır:
- Genetik Çalışmalar:
- Mendel oranlarının test edilmesi
- Genetik bağlantı analizleri
- Hardy-Weinberg dengesinin test edilmesi
- Epidemiyoloji:
- Hastalık-risk faktörü ilişkisi
- Vaka-kontrol çalışmalarının analizi
- Aşı etkinliğinin değerlendirilmesi
- Ekoloji:
- Türlerin habitat tercihlerinin incelenmesi
- Populasyon dağılımlarının analizi
- Tür çeşitliliği çalışmaları
- Fizyoloji ve Davranış:
- Davranış paternlerinin analizi
- Tercih deneyleri
- Fizyolojik yanıtların kategorik değerlendirilmesi
Hardy-Weinberg Dengesi ve Ki-kare Testi
Hardy-Weinberg dengesi, evrim geçirmeyen bir popülasyonda alel ve genotip frekanslarının sabit kalacağını belirten bir ilkedir.
Tek lokus, iki alel (A ve a) için:
- p = A alel frekansı, q = a alel frekansı (p + q = 1)
- Beklenen genotip frekansları: p² (AA), 2pq (Aa), q² (aa)
Ki-kare testi ile Hardy-Weinberg dengesi test edilebilir
Sonuçların Raporlanması
Akademik yayınlarda Ki-kare sonuçlarını nasıl raporlamalıyız?
Ki-kare Uygunluk Testi için: "Mendel’in monohybrid çaprazlama çalışmasındaki gözlenen fenotip dağılımının (sarı:yeşil) teorik 3:1 oranına uygunluğu Ki-kare uygunluk testi ile değerlendirilmiştir. Analiz sonucunda, gözlenen dağılımın teorik orana uygun olduğu bulunmuştur (χ²(1) = 0.25, p = 0.617)."
Ki-kare Bağımsızlık Testi için: "Kan grubu ile hastalık görülme sıklığı arasındaki ilişki Ki-kare bağımsızlık testi ile incelenmiştir. Analiz sonucunda, kan grubu ile hastalık arasında istatistiksel olarak anlamlı bir ilişki bulunmuştur (χ²(3) = 8.52, p = 0.036, Cramer’s V = 0.21). O kan grubuna sahip bireylerde hastalık görülme oranı, diğer kan gruplarına göre anlamlı derecede düşüktür."
Uygulama: Bitki Türü ve Habitat İlişkisi
Senaryo: Farklı bitki türlerinin farklı habitat tiplerine dağılımı arasında bir ilişki olup olmadığını test etmek istiyoruz.
Ki-kare Testi için Pratik İpuçları
- Doğru Ki-kare Testini Seçin:
- Tek değişken için teorik dağılıma uygunluk → Ki-kare Uygunluk Testi
- İki kategorik değişken arasındaki ilişki → Ki-kare Bağımsızlık Testi
- Grup karşılaştırması → Ki-kare Homojenlik Testi
- Varsayımları Kontrol Edin:
- Beklenen frekansların %80’i 5’ten büyük olmalı
- Hiçbir beklenen frekans 1’den küçük olmamalı
- Gözlemler bağımsız olmalı
- Küçük Örneklemlerde Dikkatli Olun:
- 2×2 tablolarda Yates düzeltmesini kullanın
- Fisher’ın Kesin Testini alternatif olarak düşünün
- Gerekirse kategorileri birleştirin
- Anlamlı Sonuçlar İçin İlişkinin Gücünü Değerlendirin:
- Cramer’s V veya Phi katsayısı gibi etki büyüklüğü ölçülerini kullanın
- İstatistiksel anlamlılığın yanında biyolojik anlamlılığı da yorumlayın
Soru 1
Kan grupları ile ilgili yapılan bir çalışmada 400 kişiden toplanan veriler şu şekildedir:
- A grubu: 180 kişi
- B grubu: 90 kişi
- AB grubu: 30 kişi
- O grubu: 100 kişi
Normal teorik dağılım %40 A, %10 B, %5 AB ve %45 O grubu şeklindedir. Bu dağılımın teorik dağılıma uyup uymadığını test ediniz.
Soru 2
Bir moleküler biyolog, iki gen arasında bağlantı olup olmadığını test etmek istiyor. F2 neslinde gözlenen fenotipik oranlar şöyledir:
- A-B-: 120 birey
- A-bb: 40 birey
- aaB-: 35 birey
- aabb: 5 birey
Bağımsız kalıtım hipotezini (9:3:3:1 oranı) test ediniz.