Ders 5: t-Testi ve Örneklerle Uygulamaları
MBG1032 - Doç.Dr. Alper YILMAZ
Özet
- t-testi nedir ve ne zaman kullanılır?
- t-dağılımı ve normal dağılım arasındaki fark
- t-testi türleri (tek örneklem, bağımsız örneklemler, eşleştirilmiş örneklemler)
- t-testi varsayımları
- R ile t-testi uygulamaları
- t-testi sonuçlarının yorumlanması ve raporlanması
- Biyolojide t-testi uygulamaları
t-testi Nedir?
t-testi, iki grup ortalaması arasındaki farkın istatistiksel anlamlılığını değerlendirmek için kullanılan yaygın bir parametrik testtir.
Kullanım Amacı:
- Popülasyon standart sapması bilinmediğinde ortalamaları karşılaştırmak
- Küçük örneklem boyutlarında (n < 30) bile kullanılabilir
- Deneysel verilerin istatistiksel analizinde sıklıkla kullanılır
Temel Fikir:
Gözlemlenen farkın, rastgele şans eseri ortaya çıkıp çıkmadığını değerlendirmek.
Normal Dağılım vs. t-Dağılımı
- Normal Dağılım (Z-dağılımı):
- Popülasyon parametreleri (μ, σ) bilindiğinde kullanılır
- Simetrik, çan şeklindedir
- Standart normal dağılım: N(0,1)
- t-Dağılımı:
- Popülasyon standart sapması (σ) bilinmediğinde kullanılır
- Normal dağılıma benzer ancak “kuyrukları” daha kalındır
- Örneklem büyüklüğüne (serbestlik derecesine) bağlıdır
- n büyüdükçe normal dağılıma yakınsar
t-Dağılımı ve Serbestlik Derecesi
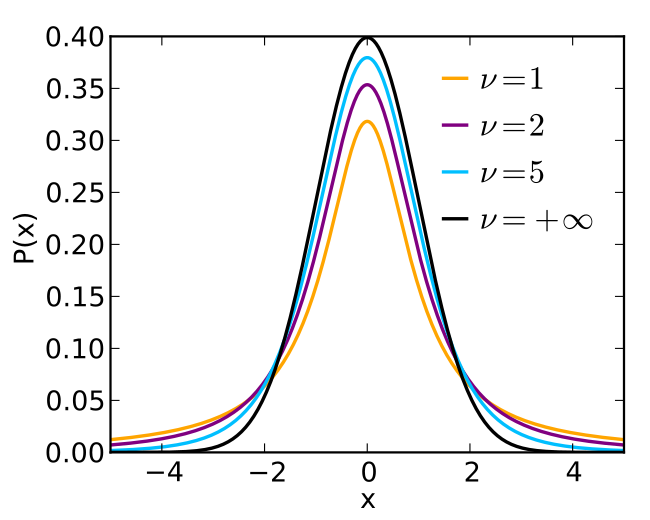
Serbestlik Derecesi (SD = n-1): Veriler üzerinde yapılabilen bağımsız karşılaştırmaların sayısı.
Görsel Kaynak: Wikimedia Commons
t-testi Çeşitleri
- Tek Örneklem t-testi:
- Bir örneklem ortalamasının bilinen bir değerle karşılaştırılması
- Örnek: “İlaç verilen hastaların ortalama kan şekeri 100 mg/dL’den farklı mı?”
- Bağımsız Örneklemler t-testi (İki Örneklem t-testi):
- İki bağımsız grubun ortalamalarının karşılaştırılması
- Örnek: “İlaç A ve İlaç B’nin ortalama etkinliği arasında fark var mı?”
- Eşleştirilmiş Örneklemler t-testi (Bağımlı t-testi):
- Aynı örneklemdeki farklı koşulların karşılaştırılması
- Örnek: “Hastaların tedavi öncesi ve sonrası değerleri arasında fark var mı?”
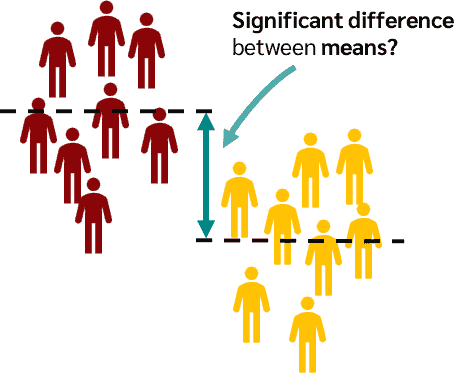
Kaynak: t-Test DATAtab
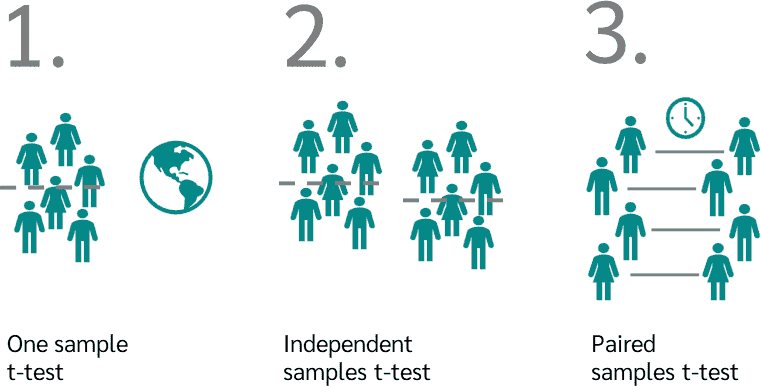
Kaynak: t-Test DATAtab
t-testi Formülleri
1. Tek Örneklem t-testi: \[ t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}} \]
2. Bağımsız Örneklemler t-testi: \[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \]
3. Eşleştirilmiş Örneklemler t-testi: \[ t = \frac{\bar{d}}{s_d/\sqrt{n}} \]
Formüller
Burada:
- \(\bar{x}\): Örneklem ortalaması
- \(\mu_0\): Test edilen popülasyon değeri
- \(s\): Örneklem standart sapması
- \(n\): Örneklem büyüklüğü
- \(\bar{d}\): Eşleştirilmiş farklılıkların ortalaması
- \(s_d\): Eşleştirilmiş farklılıkların standart sapması
t-testi Varsayımları
t-testi parametrik bir testtir ve bazı varsayımlar üzerine kuruludur:
Normallik: Verilerin normal dağılıma sahip olması veya örneklem boyutunun yeterince büyük olması (n>30)
Varyansların homojenliği: Bağımsız örneklemler t-testinde, grupların varyanslarının benzer olması
Bağımsızlık: Gözlemlerin birbirinden bağımsız olması
Ölçüm düzeyi: Verilerin aralıklı veya oransal ölçek düzeyinde olması
Not: Eğer varsayımlar karşılanmazsa, parametrik olmayan alternatifler düşünülmelidir (ör. Mann-Whitney U testi, Wilcoxon işaretli sıra testi).
t-testi Varsayımları (Bağımsızlık)
Bu varsayım, t-testi için toplanan verilerdeki bir ölçümün, diğer ölçümleri etkilememesi gerektiği anlamına gelir. Yani bir deney katılımcısının veya örneğin verdiği sonuç, diğer katılımcıların veya örneklerin sonuçlarını etkilememelidir.
- Bağımsız gözlemlere örnekler
- Farklı farelerden alınan kan örnekleri (her fare bağımsız bir birey)
- Farklı petri kaplarında yetiştirilen bakteri kolonileri
- Farklı hastalardan alınan doku örnekleri
- Rastgele seçilen 20 ağaçtan ölçülen yaprak büyüklükleri
- Bağımsız OLMAYAN gözlemlere örnekler
- Aynı fareden günlük olarak alınan ardışık kan örnekleri (bir gündeki ölçüm, diğer günü etkileyebilir)
- Aynı bakterinin farklı zamanlardaki üreme hızları
- Aynı aileden alınan genetik örnekler (genetik yakınlık nedeniyle bağımsız değil)
- Yan yana büyüyen bitkilerden alınan ölçümler (birbirlerinin büyümesini etkileyebilirler)
Tek Yönlü ve Çift Yönlü t-testi
Her t-testi, alternatif hipotezin yapısına göre tek yönlü veya çift yönlü olabilir:
Çift Yönlü t-testi (Two-sided):
- Alternatif hipotez: “eşit değildir” (\(\neq\))
- Örnek: \(H_1: \mu \neq \mu_0\) veya \(H_1: \mu_1 \neq \mu_2\)
- İlgilendiğimiz şey farkın yönü değil, sadece bir fark olup olmadığıdır
- R’da varsayılan seçenek:
alternative = "two.sided"
Tek Yönlü t-testi (One-sided):
- Alternatif hipotez: “küçüktür” (<) ya da “büyüktür” (>)
- Örnekler:
- \(H_1: \mu < \mu_0\) (
alternative = "less") - \(H_1: \mu > \mu_0\) (
alternative = "greater")
- \(H_1: \mu < \mu_0\) (
- İlgilendiğimiz durum farkın belirli bir yönde olup olmadığıdır
- Tek yönlü testler, belirli bir yönde fark beklediğimizde daha güçlüdür
Önemli Not: Tek yönlü test kullanmak için, hipotez kurulmadan önce farkın yönüne dair güçlü bir teorik gerekçe olmalıdır. Veriler incelendikten sonra tek yönlü test seçmek, tip I hata olasılığını artırır.
Tek Örneklem t-testi
Bir örneklemin ortalamasını, bilinen veya hipotez edilen bir popülasyon değeriyle karşılaştırır.
Örnek Senaryo: Yeni geliştirilen bir bitkisel ilacın, farelerde ortalama kan glikoz seviyesini referans değer olan 100 mg/dL’den farklı bir seviyeye değiştirip değiştirmediğini test etmek istiyoruz.
- \(H_0: \mu = 100\) mg/dL (İlaç, kan glikoz seviyesini değiştirmez)
- \(H_1: \mu \neq 100\) mg/dL (İlaç, kan glikoz seviyesini değiştirir)
R ile Tek Örneklem t-testi
İlacın test edildiği 15 farenin kan glikoz seviyelerini analiz edelim:
Sonucun Yorumlanması
Yorum: p-değeri 0.05’ten küçük olduğu için H0 hipotezini reddediyoruz. Bitkisel ilacın, farelerin kan glikoz seviyelerini, referans değer olan 100 mg/dL’den anlamlı şekilde düşürdüğünü söyleyebiliriz (t(14) = -11.94, p < 0.001).
Bağımsız İki Örneklem t-Testi
İki farklı, bağımsız grubun ortalamalarını karşılaştırmak için kullanılır.
Örnek Senaryo: İki farklı gübre türünün (A ve B) domates bitkilerinin boyları üzerindeki etkisini karşılaştırmak istiyoruz.
- \(H_0: \mu_A = \mu_B\) (İki gübre arasında fark yok)
- \(H_1: \mu_A \neq \mu_B\) (İki gübre arasında fark var)
R ile Bağımsız İki Örneklem t-Testi
Görselleştirme ve Yorum
Yorum: p-değeri 0.05’ten küçük olduğundan H0 hipotezini reddediyoruz. Gübre B’nin, domates bitkilerinin boyunu, Gübre A’ya göre istatistiksel olarak anlamlı şekilde daha fazla artırdığını söyleyebiliriz (t(18) = -5.14, p < 0.001).
Eşleştirilmiş Örneklemler t-Testi
Aynı deneklerin/örneklerin iki farklı durumda ölçülen değerlerini karşılaştırmak için kullanılır.
Örnek Senaryo: 10 hastanın, belirli bir ilaç tedavisinden önce ve sonra kolesterol seviyelerini karşılaştırmak istiyoruz.
- \(H_0: \mu_d = 0\) (Tedavi öncesi ve sonrası arasında fark yok)
- \(H_1: \mu_d \neq 0\) (Tedavi öncesi ve sonrası arasında fark var)
Burada \(\mu_d\), tedavi öncesi ve sonrası değerler arasındaki farkların ortalamasıdır.
R ile Eşleştirilmiş Örneklemler t-Testi
Görselleştirme ve Yorum
Yorum: p-değeri 0.05’ten küçük olduğundan H0 hipotezini reddediyoruz. İlaç tedavisinin, hastaların kolesterol seviyelerini istatistiksel olarak anlamlı şekilde düşürdüğünü söyleyebiliriz (t(9) = 14.41, p < 0.001). Ortalama düşüş 19.2 mg/dL’dir.
t-Testi Sonuçlarının Raporlanması
Akademik yayınlarda t-testi sonuçlarını nasıl raporlamalıyız?
1. Tek Örneklem t-Testi: “Bitkisel ilacın farelerin kan glikoz seviyelerine etkisi, tek örneklem t-testi ile değerlendirilmiştir. Farelerin ortalama kan glikoz seviyesi (M = 92.1, SD = 2.6) referans değerden (100 mg/dL) anlamlı şekilde düşüktür, t(14) = -11.94, p < 0.001.”
2. Bağımsız İki Örneklem t-Testi: “Gübre B ile yetiştirilen domates bitkilerinin boyları (M = 78.3 cm, SD = 3.4), Gübre A ile yetiştirilen bitkilerden (M = 71.5 cm, SD = 3.7) anlamlı şekilde daha yüksektir, t(18) = -5.14, p < 0.001.”
3. Eşleştirilmiş Örneklemler t-Testi: “İlaç tedavisi sonrası hastaların kolesterol seviyeleri (M = 230.8 mg/dL, SD = 11.0), tedavi öncesine (M = 250.0 mg/dL, SD = 7.6) göre anlamlı şekilde daha düşüktür, t(9) = 14.41, p < 0.001. Ortalama azalma 19.2 mg/dL’dir (%95 GA [16.2, 22.2]).”
Biyolojide t-Testi Uygulamaları
- Gen ekspresyonu: İki farklı koşulda gen ekspresyon seviyelerini karşılaştırma
- İlaç etkinliği: Tedavi grubunun kontrol grubuyla karşılaştırılması
- Büyüme çalışmaları: Farklı besin ortamlarında bakterilerin büyüme hızlarının karşılaştırılması
- Enzim aktivitesi: Farklı pH değerlerinde enzim aktivitelerinin karşılaştırılması
- Biyobelirteç seviyeleri: Hasta ve sağlıklı gruplar arasındaki biyobelirteç seviyelerinin karşılaştırılması
Örnek: “miR-21 ekspresyon seviyesi, kanser hastalarında (M = 4.2, SD = 1.1) sağlıklı kontrollere (M = 1.8, SD = 0.7) göre anlamlı şekilde daha yüksekti, t(58) = 10.73, p < 0.001, ortalama fark = 2.4 kat (%95 GA [2.0, 2.8]).”
Gerçek Veri Üzerinde Uygulama: iris Veri Seti
Şimdi, iris veri setinde farklı türlerdeki çiçeklerin taç yaprak (petal) boylarını karşılaştıralım.
Görselleştirme ve Yorum
Yorum: İki Iris türü arasındaki taç yaprak boyu farkı istatistiksel olarak anlamlıdır, t(86.7) = -39.5, p < 0.001. Versicolor türünün taç yaprakları (M = 4.26 cm, SD = 0.47), setosa türünün taç yapraklarından (M = 1.46 cm, SD = 0.17) ortalama 2.8 cm daha uzundur (%95 GA [2.66, 2.94]).
t-Testi için Pratik İpuçları
- Veri Hazırlığı:
- Aykırı değerleri belirleyin ve nasıl ele alacağınıza karar verin
- Verilerin normal dağılıma uygunluğunu kontrol edin (histogram, Q-Q plot, Shapiro-Wilk testi)
- Test Seçimi:
- Doğru t-testi türünü seçin (tek örneklem, bağımsız, eşleştirilmiş)
- Varsayımlar karşılanmıyorsa, parametrik olmayan alternatifleri düşünün
- Sonuçların Yorumlanması:
- Sadece p-değerine değil, etki büyüklüğüne de bakın (Cohen’s d)
- Güven aralıklarını rapor edin
- Bulgularınızı biyolojik bağlamda yorumlayın
t-Testi ile İlgili Yaygın Yanılgılar
- “p > 0.05 ise, iki grup arasında fark yoktur”
- Doğrusu: H0’ı reddedemeyiz, ancak bu “fark yoktur” anlamına gelmez
- “p < 0.05 ise, sonuç pratik olarak önemlidir”
- Doğrusu: İstatistiksel anlamlılık, pratik önemi garanti etmez
- “t-testi, her tür veri için uygundur”
- Doğrusu: t-testi, varsayımları karşılayan verilerde kullanılmalıdır
- “Örneklem büyüklüğü arttıkça, sonuçlar daha doğru olur”
- Doğrusu: Büyük örneklemler küçük farkları bile anlamlı gösterebilir
Yanılgı 4
Bu yanılgıyla ilgili doğru açıklama: “Büyük örneklemler küçük farkları bile anlamlı gösterebilir” şeklindedir. İstatistiksel açıdan bakıldığında, örneklem büyüklüğü arttıkça istatistiksel testlerin gücü (power) artar. Yani, gerçekten var olan bir etkiyi tespit etme olasılığımız yükselir. Bu doğrudur ve istatistiğin temel ilkelerinden biridir. Ancak buradaki yanılgı şudur:
- İstatistiksel anlamlılık ≠ Pratik anlamlılık: Örneklem büyüklüğü arttıkça, çok küçük ve pratikte önemsiz farklar bile istatistiksel olarak anlamlı çıkabilir. Örneğin:
- 10 fare ile yapılan bir deneyde 5 mg/dL’lik bir kan şekeri farkı istatistiksel olarak anlamlı çıkmayabilir.
- 1000 fare ile aynı deneyi yaptığınızda 1 mg/dL’lik bir fark bile istatistiksel olarak anlamlı çıkabilir. Ancak 1 mg/dL’lik fark biyolojik olarak anlamlı mıdır? Bu kadar küçük bir fark gerçekten önemli midir?
- Yanlılık (bias) sorunu: Örneklem büyüklüğü, sistematik hatayı (bias) azaltmaz. Eğer örneklem seçiminizde bir yanlılık varsa, örneklem büyüklüğünü artırmak bu sorunu çözmez, hatta daha da belirginleştirebilir.
R’da t-Testi Kullanımı (Özet)
# 1. Tek Örneklem t-Testi
# a. Çift yönlü test (varsayılan)
t.test(x, mu = 0)
# b. Tek yönlü test (küçüktür)
t.test(x, mu = 0, alternative = "less")
# c. Tek yönlü test (büyüktür)
t.test(x, mu = 0, alternative = "greater")R’da t-Testi Kullanımı (Özet)
# 2. Bağımsız İki Örneklem t-Testi
# a. Varyansların eşit olduğu varsayımıyla
t.test(x, y, var.equal = TRUE)
# b. Varyansların eşit olmadığı varsayımıyla (Welch t-testi, var
sayılan)
t.test(x, y)
# c. Tek yönlü test ile (örneğin x'in y'den büyük olup olmadığın
ı test etmek için)
t.test(x, y, alternative = "greater")R’da t-Testi Kullanımı (Özet)
# 3. Eşleştirilmiş Örneklemler t-Testi
t.test(x, y, paired = TRUE)
# Tek yönlü seçeneği ile
t.test(x, y, paired = TRUE, alternative = "greater")R’da t-Testi Kullanımı (Özet)
# 4. Formül kullanımı (veritabanları ile çalışırken)
t.test(value ~ group, data = mydata)
t.test(value ~ group, data = mydata, paired = TRUE)
t.test(value ~ group, data = mydata, alternative = "less")Farklı t-Test Türleri için Varsayımlar ve R Kod Örnekleri
| t-Testi Türü | Temel Varsayımlar | R Kodu |
|---|---|---|
| Tek Örneklem | - Verilerin normal dağılması veya n>30 - Bağımsız gözlemler |
t.test(x, mu = 0) |
| Bağımsız İki Örneklem (eşit varyans) |
- İki grupta da normal dağılım - Varyansların homojenliği - Bağımsız gözlemler |
t.test(x, y, var.equal = TRUE) |
| Bağımsız İki Örneklem (Welch/eşit olmayan varyans) |
- İki grupta da normal dağılım - Varyanslar farklı olabilir - Bağımsız gözlemler |
t.test(x, y) |
| Eşleştirilmiş Örneklemler | - Farkların normal dağılması - Eşleştirilmiş gözlemler |
t.test(x, y, paired = TRUE) |