Bir deneyde, bir olayın gerçekleşme olasılığı istenilen durumların sayısının, tüm olası durumların sayısına oranlanmasıdır.
Formül:
\[
P(A) = \frac{s(A)}{s(E)}
\]
P(A): Olasılık Değeri, A olayının gerçekleşme ihtimali.
s(A): İstenen Durumlar, A kümesinin eleman sayısı.
s(E): Tüm Durumlar, Evrensel kümenin (E) eleman sayısı.
Evrensel küme
Soru: İki zar aynı anda atıldığında toplamın 7 gelmesi olasılığını hesaplarken, evrensel küme ne olmalıdır?
İstenen durumların sayısı kaçtır?
Evrensel küme 2
Soru: Bir ailenin iki çocuğu var ve en az biri erkek. Diğerinin de erkek olma olasılığı nedir?
Evrensel küme sayısı ve istenen durumların sayısı kaçtır?
İstenen olay sayısı: EE
Evrensel küme: EE, EK (KK durumu kümemizde yok!)
P(diğer çocuğun erkek olması) = 1 / 2
Evrensel küme 3
Soru: Bir hastanede 10.000 kadına meme kanseri tarama testi uygulanıyor. Bu hastalığın görülme sıklığını %1 olarak kabul edelim.
Bu testin doğruluk oranı %90 — yani hasta birini %90 ihtimalle yakalar, sağlıklı birini de %90 ihtimalle doğru şekilde “sağlıklı” olarak tanır. Test sonucunuz pozitif çıktı. Gerçekten hasta olma ihtimaliniz nedir? (Tarama Testi Paradoksu)
Dağılım
Evrensel kümenin çok büyük olduğu veya sayılamadığı durumlarda dağılımlar kullanılabilir
Normal dağılım modeli
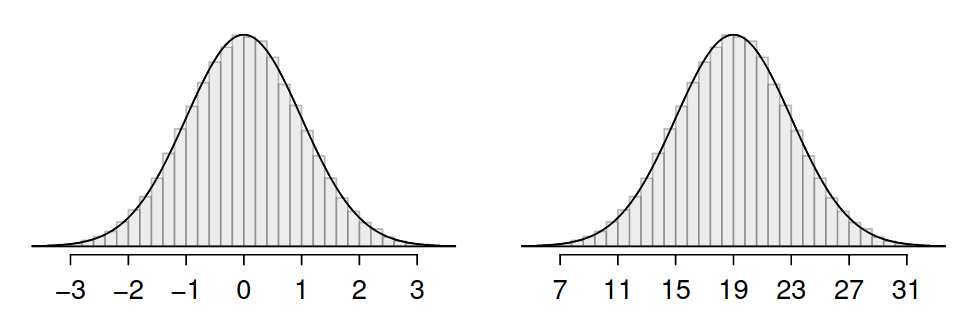
Normal dağılım kuralı
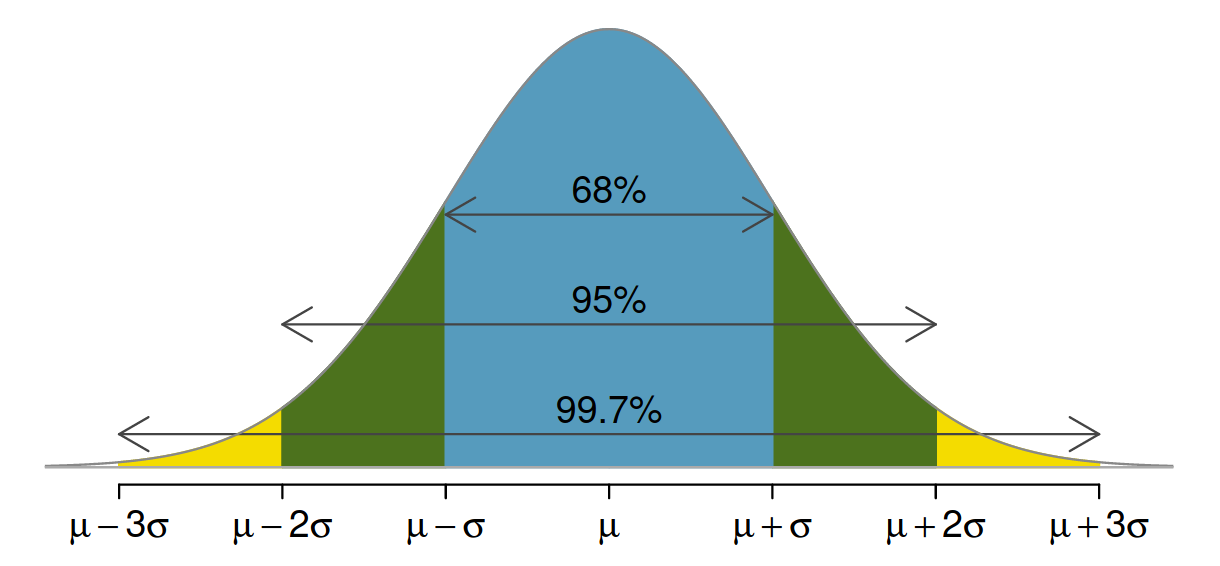
Z skor
Ortalamaya kaç standard sapma uzak olunduğunu gösterir ve normal dağılım değerlerini standart hale getirir (~ -3,3)
\[ Z = \frac{x-\mu}{\sigma} \]
Normal dağılım tablosu
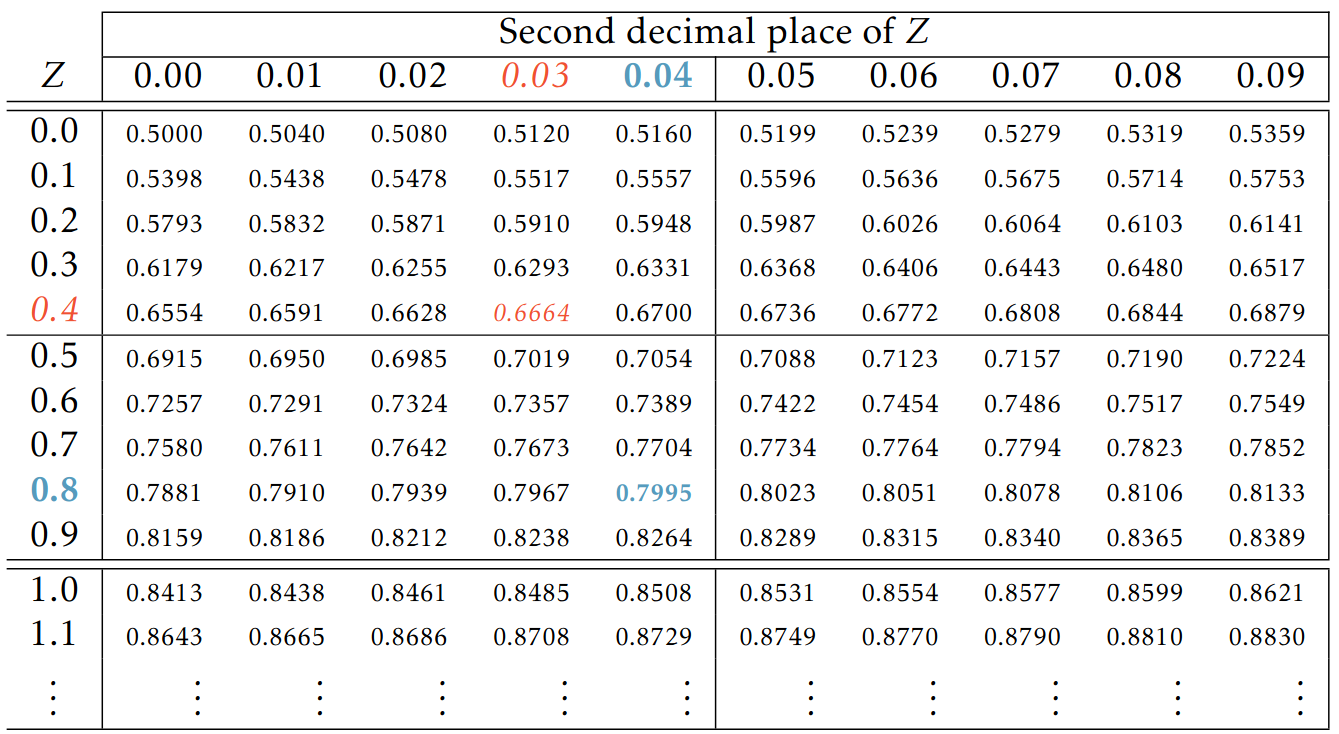
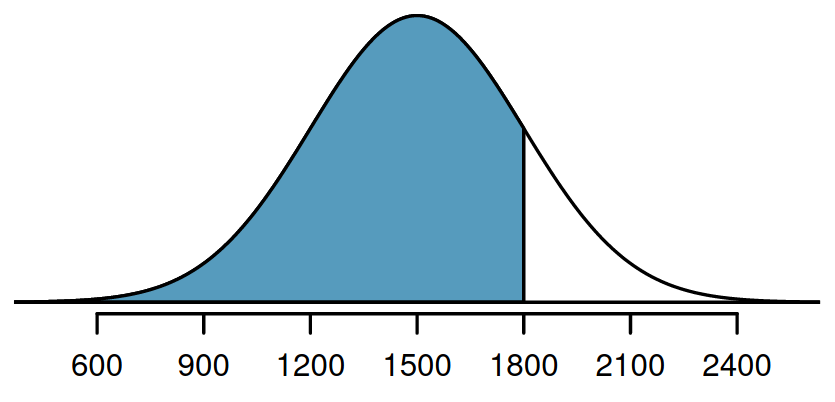
Örnek
SAT skorları için ortalama 1500, standart sapma 300 iken 1800’den düşük puan alma ihtimali kaçtır? 1800 puan yüzde kaçlık dilime denk gelmektedir?
Z-skor açısından
Örnek 2
Bir öğrencinin SAT skoru 1630’tan yüksek olma ihtimali nedir?
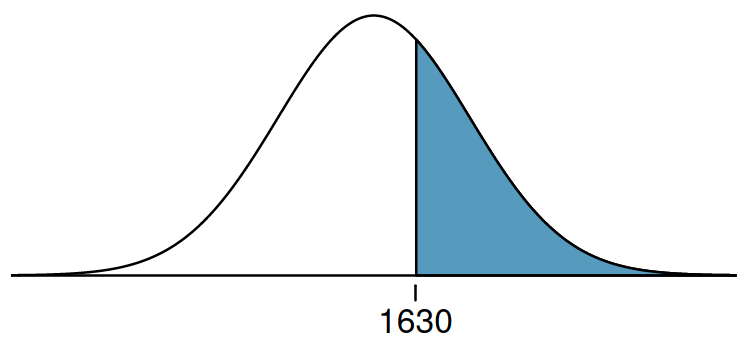
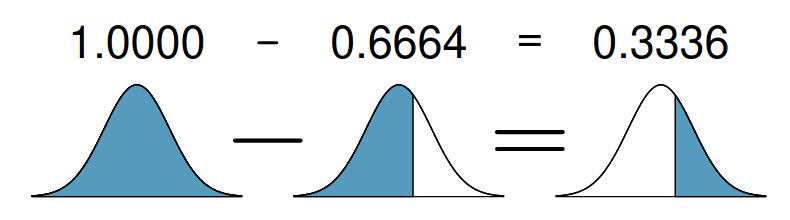
Soru
20-62 yaş erkeklerin boy dağılımı ortalaması 70 inç ve standart sapması 3.3 inç iken, rastgele seçilen bir erkeğin boyunun 69 inç ve 74 inç arasında olması ihtimali nedir?
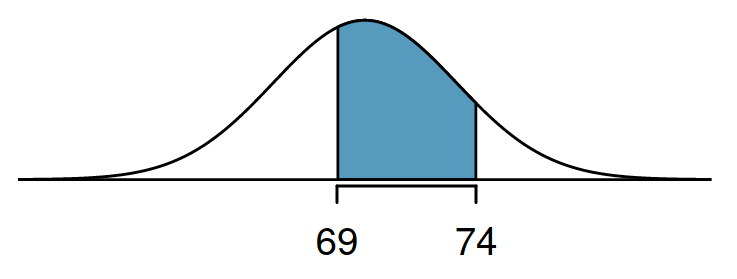
Soru
Boyu 40 yüzdelik dilimde olan bir kişinin boyu kaçtır?
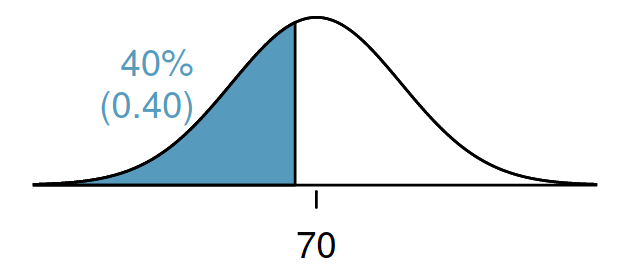
Poisson dağılımı
Poisson dağılımı, nadiren meydana gelen olayların, belirli bir zaman aralığında veya belirli bir alanda kaç kere gerçekleşeceğini tahmin etmek için kullanılan bir olasılık dağılımıdır.
Aşağıdaki grafik 8 milyon nüfuslu bir şehirde bir yıl boyunca hastaneye gelen günlük Akut Miyokard İnfarktüsü (AMI) vaka sayısını göstermektedir (ortalama=4.4 kişi)
Örnekler
Poisson dağılımı gösteren biyolojik veriler, genellikle nadir ve rastgele meydana gelen olaylara odaklanır. Bu tür veriler, çeşitli biyolojik disiplinler ve uygulama alanları üzerinden örneklerle açıklanabilir:
Mikrobiyoloji ve Bakteriyoloji:
Bakteri Kolonilerinin Sayımı: Petri kabında belirli bir süre ve koşullar altında büyüyen bakteri kolonilerinin sayımı. Örneğin, bir laboratuvar ortamında standart bir hacimdeki besiyeri üzerine ekilen bakteri spesifik bir zaman diliminde kaç koloni oluşturur.
Virüs Titrelemeleri: Bir hacimdeki virüs partikülleri sayısı. Bu, özellikle su örneklerinde veya biyolojik sıvılarda yapılan ölçümler için geçerlidir.
Ekoloji ve Koruma Biyolojisi:
Ender Türlerin Birey Sayısı: Belirli bir alandaki nadir görülen türlerin birey sayıları. Bu, büyük koruma alanlarında veya özel ekosistemlerde endemik türler için kullanılabilir.
Parazit Sayımı: Belirli bir konakçı popülasyonunda parazitlerin dağılımı. Örneğin, bir balık popülasyonunda bulunan parazit türlerinin sayısı.
Moleküler Biyoloji ve Genetik:
DNA Mutasyonları: Belirli bir gen uzunluğu boyunca meydana gelen mutasyonların sayısı. Özellikle büyük genomlar üzerinde nadiren meydana gelen olaylar için kullanılır.
Transkripsiyonel Olaylar: Belirli bir zaman diliminde hücrede meydana gelen mRNA transkripsiyon olaylarının sayısı.
Halk Sağlığı ve Epidemiyoloji:
Nadir Hastalık Vakaları: Bir bölgede belirli bir zaman diliminde görülen nadir hastalık vakalarının sayısı. Özellikle düşük prevalanslı hastalıklar için geçerlidir.
Salgın Olayları: Belirli bir zaman aralığında bir popülasyonda meydana gelen salgın hastalık vakalarının sayısı.
Nörobilim ve Fizyoloji:
Nöronal Ateşleme Olayları: Belirli bir zaman diliminde bir veya birden fazla nöronun ateşleme (aksiyon potansiyeli) olaylarının sayısı. Özellikle düşük ateşleme hızlarına sahip nöronlar için Poisson dağılımı uygulanabilir.
Sinaptik Olaylar: Sinapslarda meydana gelen nörotransmitter salınım olaylarının sayısı.
Poisson dağılımı
Poisson fonksiyonu
k olay olma ihtimali
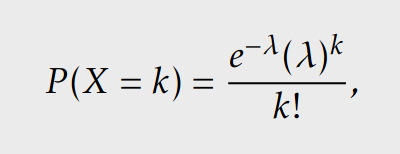
t zaman içinde gerçekleşen k olay ihtimali
Örnek
7 gün içinde 2 hastanın AMI teşhisi ile hastanelik olma ihtimali nedir? (\(\lambda\)=4.4, k=2, t=7)
7 gün içinde en fazla 2 kişinin hastanelik olması ihtimali nedir?
En az 3 kişinin 7 gün içinde hastanelik olma ihtimali kaçtır?
Bernoulli dağılımı
Bernoulli dağılımı, yalnızca iki sonuçtan (başarı veya başarısızlık, evet veya hayır, 1 veya 0 gibi) birini alabilen rastgele bir deneyi modellemek için kullanılan bir olasılık dağılımıdır. Binomial dağılımında n defa gerçekleşen, ikili sonucu olan olayların ihtimali hesaplanırken, Bernoulli dağılımında k=1’dir.
Madeni para atışı, hastalık testi sonucu, bitki tohumu çimlenmesi, ilaç tepkisi gibi örnekler Bernoulli dağılımı için örnek gösterilebilir.
Bernoulli dağılımının tekrarı ile sadece Binomial dağılım ortaya çıkmaz; geometrik, negatif binomial ve hipergeometrik dağılımlar Bernoulli dağılımı temel alır.
Binomial dağılım
Binomial dağılım, bağımsız ve aynı olasılığa sahip n denemede tam olarak k başarı elde etme olasılığını hesaplamak için kullanılan bir olasılık dağılımıdır. Her deneme bir Bernoulli denemesidir (iki sonuç: başarı veya başarısızlık).
Aşağıdaki grafik 10 hastaya uygulanan bir tedavide yan etki görülme sayısının dağılımını göstermektedir (yan etki olasılığı p=0.3)
Örnekler
Binomial dağılım, sabit sayıda bağımsız denemede başarı sayısını modellemek için kullanılır. Biyolojik ve biyomedikal araştırmalarda sıkça karşılaşılan örnekler:
Genetik ve Popülasyon Genetiği:
Hardy-Weinberg Genotip Frekansları: Bir popülasyonda belirli bir allelin 2n kromozomdan kaç tanesinde bulunacağı. Örneğin, heterozigot taşıyıcı sıklığının hesaplanması.
SNP Allel Frekansları: Bir örneklemdeki bireylerin kaç tanesinin belirli bir varyantı taşıdığı.
Klinik Araştırmalar ve Farmakoloji:
Tedaviye Yanıt Oranları: n hastadan kaç tanesinin tedaviye yanıt vereceği. Örneğin, 20 hastaya uygulanan bir kemoterapide tam yanıt gösteren hasta sayısı.
Yan Etki İnsidansı: Bir ilacın n hastada kaç tanesinde yan etki oluşturduğu.
Mikrobiyoloji:
Antibiyotik Duyarlılık Testleri: n bakteri izolatından kaç tanesinin belirli bir antibiyotiğe dirençli olduğu.
Aşı Etkinliği: Aşılanan n kişiden kaç tanesinin enfeksiyondan korunduğu.
Epidemiyoloji:
Hastalık Prevalansı: Rastgele seçilen n kişilik bir örneklemde kaç kişinin belirli bir hastalığa sahip olduğu.
Tarama Testi Sonuçları: n kişiye uygulanan tarama testinde kaç pozitif sonuç çıkacağı.
Ekoloji:
Tohum Çimlenmesi: Ekilen n tohumdan kaç tanesinin çimleneceği, her tohumun bağımsız ve aynı çimlenme olasılığına sahip olduğu varsayımıyla.
Binomial dağılım
Binomial fonksiyonu
n denemede k başarı olma ihtimali
\[ P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} \]
Beklenen değer (ortalama) ve varyans
\[ E(X) = np \qquad \text{Var}(X) = np(1-p) \]
Kombinasyon formülü
\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \]
Örnek
10 hastaya bir tedavi uygulanıyor. Yan etki olasılığı p=0.3 iken, tam olarak 3 hastada yan etki görülme ihtimali nedir?
10 hastadan en fazla 2 tanesinde yan etki görülme ihtimali nedir?
En az 5 hastada yan etki görülme ihtimali kaçtır?
Negatif binomial dağılım
Negatif binomial dağılım, bağımsız Bernoulli denemelerinde r. başarıya ulaşmak için gereken toplam deneme sayısını modelleyen bir olasılık dağılımıdır. Geometrik dağılımın genellemesidir: geometrik dağılımda r=1 iken, negatif binomial dağılımda r≥1’dir.
Aşağıdaki grafik bir klinik araştırmada tedaviye yanıt oranı p=0.3 iken, 3. yanıt veren hastayı bulmak için gereken toplam hasta sayısının dağılımını göstermektedir.
Örnekler
Negatif binomial dağılım, belirli sayıda başarıya ulaşmak için gereken deneme sayısını veya aşırı dağılmış (overdispersed) sayım verilerini modellemek için kullanılır. Biyolojik araştırmalarda sıkça karşılaşılan örnekler:
Klinik Araştırmalar:
Hasta Tarama Süreci: Bir klinik çalışmaya dahil edilecek kriterleri karşılayan r hasta bulmak için kaç aday taranması gerektiği. Örneğin, nadir bir hastalığı olan 5 uygun hastayı bulmak için gereken tarama sayısı.
Tedaviye Yanıt: Belirli sayıda başarılı tedavi sonucu elde etmek için kaç hastanın tedavi edilmesi gerektiği.
Genomik ve RNA-seq:
Gen Ekspresyon Sayımları: RNA-seq verilerinde gen başına okunan read sayıları genellikle Poisson’dan daha fazla varyans gösterir (overdispersion). Negatif binomial dağılım bu fazla varyansı modellemek için standart yöntemdir. DESeq2 ve edgeR gibi yaygın araçlar negatif binomial model kullanır.
Ekoloji:
Tür Zenginliği Örneklemesi: Belirli sayıda nadir türü gözlemlemek için gereken örnekleme çabası. Örneğin, bir ekosistemde 3 farklı endemik kuş türünü gözlemlemek için yapılması gereken arazi çalışması sayısı.
Parazit Yükü: Konakçılar arasındaki parazit sayısı dağılımı genellikle Poisson’dan daha dağınıktır ve negatif binomial ile daha iyi modellenir.
Epidemiyoloji:
Hastalık Kümelenmeleri: Belirli bir bölgede hastalık vakalarının sayısı Poisson’dan daha fazla varyans gösterdiğinde (bazı bölgelerde kümelenme, bazılarında hiç vaka yokken) negatif binomial dağılım kullanılır.
Kalite Kontrol ve Mikrobiyoloji:
Kontaminasyon Tespiti: Üretim hattında r. kusurlu ürünü bulmak için kaç ürünün incelenmesi gerektiği.
Not: R’da rnbinom ve dnbinom fonksiyonları r. başarıdan önceki başarısızlık sayısını (x = k − r) kullanır; toplam deneme sayısını değil.
Örnek
Tedaviye yanıt oranı p=0.3 iken, 3. yanıt veren hastanın tam olarak 10. hasta olma ihtimali nedir? (yani 7 başarısızlık + 3. başarı)
3 başarılı tedavi için en fazla 8 hasta tedavi etme ihtimali nedir? (yani en fazla 5 başarısızlık)
3 başarılı tedavi için 15’ten fazla hasta tedavi etme ihtimali kaçtır? (yani 12’den fazla başarısızlık)
Geometik dağılım
Geometrik dağılım, bağımsız ve aynı şekilde dağılmış Bernoulli denemeleri serisinde, ilk başarının elde edilmesi için gereken deneme sayısını modelleyen bir olasılık dağılımıdır. Diğer bir deyişle, bir dizi denemede ilk başarıya ulaşana kadar yapılan deneme sayısının dağılımını tanımlar.
Örnekler
Geometrik dağılım, biyolojik süreçler ve fenomenler içinde çeşitli örneklerle temsil edilebilir. Bu tür dağılımlar, belirli bir olayın meydana gelmesi için gereken deneme sayısını veya bir başarı elde edene kadar geçen süreyi modellemek için özellikle uygun olabilir. İşte geometrik dağılımı kullanarak modelleyebileceğiniz biyolojik örnekler:
Hastalığa Dirençli Bitki Bulma: Bir araştırmacı, belirli bir hastalığa dirençli bir bitki çeşidi geliştirmek üzere rastgele mutasyonlar oluşturuyor. Her bir mutasyonun, istenilen direnci gösterme olasılığı düşük olabilir. Bu durumda, araştırmacının dirençli bir mutasyon elde etmesi için gereken deneme sayısı geometrik dağılımla modelleyebilir.
Nadir Görülen Türlerin Tespiti: Bir ekolog, nadir görülen bir türün üyelerini bulmak için rastgele örnekler alıyor. Her bir örnekleme denemesinde bu türden bir birey bulma şansı düşükse, bu tür bir bireyin ilk kez tespit edilmesi için gereken örnekleme sayısı geometrik dağılımla modelleyebilir.
Antibiyotik Direnci: Bir mikrobiyolog, bir bakteri popülasyonundan rastgele seçilen bir bakterinin belirli bir antibiyotiğe dirençli olup olmadığını test eder. Eğer popülasyon içinde dirençli bakterilerin oranı düşükse, ilk dirençli bakterinin tespit edilmesi için yapılması gereken test sayısı geometrik dağılımla ifade edilebilir.
Genetik Çaprazlamalar: Genetik bir özelliğin baskın olduğu durumda, belirli bir çaprazlama sonucunda istenilen genetik yapıya (örneğin, bir hastalığa karşı dirençli bir genotip) sahip bir yavru elde edilene kadar gereken çaprazlama sayısı. Her bir çaprazlamanın bağımsız ve sabit bir başarı şansı varsa, bu durum geometrik dağılımla modellenebilir.
Geometrik dağılım
Gerçekleşme ihtimali p= 0.35 iken, ilk denemede başarılı olma ihtimali yine 0.35’tir. İkinci denemede başarılı olma ihtimali ise 0.65 x 0.35 = 0.228i’dir. Üçüncü denemede başarılı olma ihtimali ise 0.65 x 0.65 x 0.35 = 0.148’tir.
Geometric dağılımda olasılık üssel şekilde azalır.
Geometrik dağılım
k. denemede ilk başarıyı elde etme ihtimali
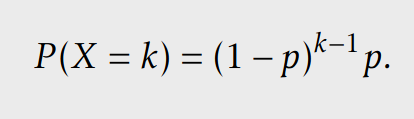
Bekleme süresinin ortalaması, varyansı ve standard sapması
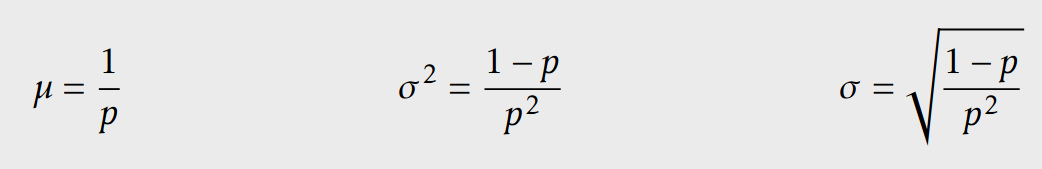
Geometrik dağılım - formüller
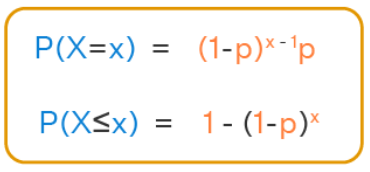
Soru
Başarının ilk 4 denemede gerçekleşme ihtimali kaçtır?
P(X=1) + P(X=2) + P(X=3) + P(X=4) = 0.82
Başarının ilk 4 denemede gerçekleşmeme ihtimali kaçtır?
1- 0.82 = 0.18
R’da geometrik fonksiyon “başarıdan öncde gerekli deneme sayısını” dikkate alır
Özet
Normal dağılım (sürekli) →
Poisson (kesikli, nadir olaylar)
Bernoulli (yapı taşı)
Bernoulli türevleri: Binomial (n kez tekrar)
Geometrik (ilk başarıya kadar)
Negatif Binomial (r. başarıya kadar, geometriğin genellemesi)
Log-Normal (sürekli, biyolojik verilerde çok yaygın)
Hipergeometrik dağılım
Hipergeometrik dağılım, sonlu bir popülasyondan iadesiz çekiliş yapıldığında, belirli bir özelliğe sahip bireylerin seçilme sayısını modelleyen bir olasılık dağılımıdır. Binomial dağılımdan farkı, her çekişte olasılığın değişmesidir çünkü çekilen birey geri konmaz.
Aşağıdaki grafik bir gen seti zenginleştirme analizini göstermektedir: 20.000 genlik genomdan rastgele 50 gen seçildiğinde, bunların kaç tanesinin kanser ilişkili 800 gen arasından geldiğini sorgulamaktadır.
Örnekler
Hipergeometrik dağılım, iadesiz örneklemde belirli bir kategoriden kaç birey seçileceğini modellemek için kullanılır. Biyolojik araştırmalarda yaygın kullanım alanları:
Biyoinformatik ve Genomik:
Gen Ontolojisi (GO) Zenginleştirme Analizi: Diferansiyel olarak ifade edilen gen listesinde belirli bir biyolojik yolağa ait genlerin beklenenden fazla olup olmadığının testi. Örneğin, 200 upregüle genin 15’inin apoptoz yolağında olması tesadüf mü?
KEGG Pathway Analizi: Bir gen listesindeki metabolik yolak zenginleştirmesinin istatistiksel anlamlılığı.
Genetik ve Popülasyon Biyolojisi:
Fisher’ın Kesin Testi (Fisher’s Exact Test): 2x2 kontenjans tablolarında beklenen frekanslar düşük olduğunda kullanılan test, hipergeometrik dağılıma dayanır.
Genetik Sürüklenme Modelleri: Küçük popülasyonlarda allel frekanslarının nesiller arası değişimi, iadesiz örnekleme olarak modellenebilir.
Ekoloji:
Yakalama-Tekrar Yakalama Yöntemi: Bir gölde 100 balık işaretlenip bırakıldıktan sonra, tekrar yakalanan 50 balıktan kaç tanesinin işaretli olduğu.
Biyoçeşitlilik Örneklemesi: Bir alandaki toplam türlerin bilinen bir alt kümesinin rastgele örneklemde temsil oranı.
Klinik Araştırmalar:
Rastgele Hasta Seçimi: 100 kişilik bir kohorttan (40 kadın, 60 erkek) 20 kişilik bir tedavi grubu oluşturulduğunda kadın sayısının dağılımı.
Kalite Kontrol:
Lot Örneklemesi: 500 ürünlük bir partiden 30 ürün kontrol edildiğinde, kusurlu ürün sayısının dağılımı.
Hipergeometrik dağılım
Hipergeometrik fonksiyonu
Popülasyondaki N bireyden n tanesini seçtiğimizde, K özel bireyin k tanesini çekme ihtimali
Parametreler:N = popülasyon büyüklüğü, K = popülasyondaki “başarı” sayısı, n = çekilen örneklem, k = örneklemdeki başarı sayısı
Örnek
20.000 genlik genomda 800 tanesi kanser ilişkili. Rastgele 50 gen seçtiğimizde tam olarak 5 tanesinin kanser geni olma ihtimali nedir?
50 genlik listede 12 veya daha fazla kanser geni bulunma ihtimali nedir? (zenginleştirme p-değeri)
Fisher’ın kesin testi ile aynı sonucu elde edelim
Log-normal dağılım
Log-normal dağılım, logaritması normal dağılım gösteren bir sürekli olasılık dağılımıdır. Değerler her zaman pozitiftir ve dağılım sağa çarpıktır. Biyolojide çarpımsal süreçlerle oluşan ölçümler (hücre bölünmesi, gen ekspresyonu, enzim aktivitesi) genellikle log-normal dağılım gösterir.
Aşağıdaki grafik gen ekspresyon seviyelerinin (FPKM) ham halini ve log dönüşümü sonrasını karşılaştırmaktadır.
Örnekler
Log-normal dağılım, değerleri sıfırın altına düşmeyen ve sağa çarpık olan biyolojik ölçümlerde yaygın olarak karşımıza çıkar:
Genomik ve Transkriptomik:
Gen Ekspresyon Seviyeleri: RNA-seq verilerinde FPKM/TPM/RPKM değerleri tipik olarak log-normal dağılım gösterir. Çoğu gen düşük seviyede ifade edilirken, az sayıda gen çok yüksek seviyede ifade edilir.
Protein Konsantrasyonları: Hücre içi protein miktarları genellikle log-normal dağılır.
Farmakoloji ve Toksikoloji:
İlaç Konsantrasyonları (IC₅₀): Bir ilacın hücre büyümesini %50 inhibe eden konsantrasyonu bireyler arasında log-normal dağılım gösterir.
Doz-Yanıt Eğrileri: İlaç dozlarının etkisi genellikle logaritmik ölçekte analiz edilir.
Hücre Biyolojisi:
Hücre Büyüklükleri: Bir popülasyondaki hücrelerin çap veya hacim dağılımı. Hücreler büyüyüp bölündüğü için çarpımsal bir süreç söz konusudur.
Hücre Bölünme Süreleri: Hücrelerin bir bölünme döngüsünü tamamlama süreleri.
Ekoloji ve Çevre Bilimleri:
Tür Bolluğu: Bir ekosistemdeki türlerin birey sayıları — az sayıda tür çok baskınken, çoğu tür nadir bulunur.
Çevresel Kirletici Konsantrasyonları: Toprak veya sudaki ağır metal seviyeleri.
Epidemiyoloji:
Kuluçka Süreleri: Birçok enfeksiyon hastalığının kuluçka süresi log-normal dağılım gösterir.
